# Can the Vacuum be Engineered for Spaceflight applications? http://www.keelynet.com/gravity/putnasa.htm
Overview of Theory and Experiments ; H. E. Puthoff, Ph.D. ; Institute for Advanced Studies at Austin ; 4030 W. Braker Lane, Suite 300 ; Austin, TX 78759-5329 ; Voice (512) 346-9947, Fax (512) 346-3017, E-mail: puthoff@aol.com
From: Puthoff@aol.com ; Date: Mon, 18 Aug 1997 16:21:16 -0400 (EDT) ; To: vortex-l@eskimo.com ; Subject: Re: NASA posts the results of propulsion conference
For those interested, here is a copy of the paper I presented at the NASA Breakthrough Propulsion Physics conference at Lewis Research Center last week. – Hal Puthoff
ABSTRACT
Quantum theory predicts, and experiments verify, that empty space (the vacuum) contains an enormous residual background energy known as zero-point energy (ZPE).
Originally thought to be of significance only for such esoteric concerns as small perturbations to atomic emission processes, it is now known to play a role in large-scale phenomena of interest to technologists as well, such as the inhibition of spontaneous emission, the generation of short-range attractive forces (e.g., the Casimir force), and the possibility of accounting for sonoluminescence phenomena.
ZPE topics of interest for spaceflight applications range from fundamental issues (where does inertia come from, can it be controlled?), through laboratory attempts to extract useful energy from vacuum fluctuations (can the ZPE be “mined” for practical use?), to scientifically-grounded extrapolations concerning “engineering the vacuum” (is “warp-drive” space propulsion a scientific possibility?). Recent advances in research into the physics of the underlying ZPE indicate the possibility of potential application in all these areas of interest.
INTRODUCTION
The concept “engineering the vacuum” was first introduced by Nobel Laureate T. D. Lee in his book Particle Physics and Introduction to Field Theory. As stated there: “The experimental method to alter the properties of the vacuum may be called vacuum engineering…. If indeed we are able to alter the vacuum, then we may encounter some new phenomena, totally unexpected.” Recent experiments have indeed shown this to be the case.
With regard to space propulsion, the question of engineering the vacuum can be put succinctly: “Can empty space itself provide the solution?”
Surprisingly enough, there are hints that potential help may in fact emerge quite literally out of the vacuum of so-called “empty space.” Quantum theory tells us that empty space is not truly empty, but rather is the seat of myriad energetic quantum processes that could have profound implications for future space travel. To understand these implications it will serve us to review briefly the historical development of the scientific view of what constitutes empty space.
At the time of the Greek philosophers, Democritus argued that empty space was truly a void, otherwise there would not be room for the motion of atoms.
Aristotle, on the other hand, argued equally forcefully that what appeared to be empty space was in fact a plenum (a background filled with substance), for did not heat and light travel from place to place as if carried by some kind of medium?
The argument went back and forth through the centuries until finally codified by Maxwell’s theory of the luminiferous ether, a plenum that carried electromagnetic waves, including light, much as water carries waves across its surface. Attempts to measure the properties of this ether, or to measure the Earth’s velocity through the ether (as in the Michelson- Morley experiment), however, met with failure.
With the rise of special relativity which did not require reference to such an underlying substrate, Einstein in 1905 effectively banished the ether in favor of the concept that empty space constitutes a true void. Ten years later, however, Einstein’s own development of the general theory of relativity with its concept of curved space and distorted geometry forced him to reverse his stand and opt for a richly-endowed plenum, under the new label spacetime metric.
It was the advent of modern quantum theory, however, that established the quantum vacuum, so-called empty space, as a very active place, with particles arising and disappearing, a virtual plasma, and fields continuously fluctuating about their zero baseline values. The energy associated with such processes is called zero-point energy (ZPE), reflecting the fact that such activity remains even at absolute zero.
THE VACUUM AS A POTENTIAL ENERGY SOURCE
At its most fundamental level, we now recognize that the quantum vacuum is an enormous reservoir of untapped energy, with energy densities conservatively estimated by Feynman and others to be on the order of nuclear energy densities or greater. Therefore, the question is, can the ZPE be “mined” for practical use? If so, it would constitute a virtually ubiquitous energy supply, a veritable “Holy Grail” energy source for space propulsion.
As utopian as such a possibility may seem, physicist Robert Forward at Hughes Research Laboratories demonstrated proof-of-principle in a paper published in 1984, “Extracting Electrical Energy from the Vacuum by Cohesion of Charged Foliated Conductors.”
Forward’s approach exploited a phenomenon called the Casimir Effect, an attractive quantum force between closely-spaced metal plates, named for its discoverer, H. G. B. Casimir of Philips Laboratories in the Netherlands.
The Casimir force, recently measured with high accuracy by S. K. Lamoreaux at the University of Washington, derives from partial shielding of the interior region of the plates from the background zero-point fluctuations of the vacuum electromagnetic field.
As shown by Los Alamos theorist Milonni and his colleagues, this shielding results in the plates being pushed together by the unbalanced ZPE radiation pressures. The result is a corollary conversion of vacuum energy to some other form such as heat.
Proof that such a process violates neither energy nor thermodynamic constraints can be found in a paper by D. Cole and myself published in 1993 under the title “Extracting Energy and Heat from the Vacuum.”
Attempts to harness the Casimir and related effects for vacuum energy conversion are ongoing in our laboratory and elsewhere. The fact that its potential application to space propulsion has not gone unnoticed by the Air Force can be seen in its request for proposals for the FY-1986 Defense SBIR Program. Under entry AF86-77, Air Force Rocket Propulsion Laboratory (AFRPL) Topic: Non-Conventional Propulsion Concepts we find the statement: “Bold, new non-conventional propulsion concepts are solicited…. The specific areas in which AFRPL is interested include…. (6) Esoteric energy sources for propulsion including the zero point quantum dynamic energy of vacuum space.”
Several experimental formats for tapping the ZPE for practical use are under investigation in our laboratory. An early one of interest is based on the idea of a Casimir pinch effect in non-neutral plasmas, basically a plasma equivalent of Forward’s electromechanical charged-plate collapse (see Puthoff, 1990). The underlying physics is described in a paper submitted for publication by myself and M. Piestrup, and it is illustrative that the first of several patents issued to a consultant to our laboratory, K.R. Shoulders, contains the descriptive phrase “… energy is provided… and the ultimate source of this energy appears to be the zero-point radiation of the vacuum continuum.”
Another intriguing possibility is provided by the phenomenon of sonoluminescence, bubble collapse in an ultrasonically-driven fluid which is accompanied by intense, sub-nanosecond light radiation. Although the jury is still out as to the mechanism of light generation, Nobelist Julian Schwinger has argued for a Casimir interpretation. Possibly related experimental evidence for excess heat generation in ultrasonically-driven cavitation in heavy water is claimed in an EPRI Report by George and Stringham of E-Quest Sciences, although attributed to a nuclear micro- fusion process. Work is under way in our laboratory to see if this claim can be replicated.
Yet another proposal for ZPE extraction is described in a patent issued to Mead and Nachamkin. The approach proposes the use of resonant dielectric spheres, slightly detuned from each other, to provide a beat-frequency downshift of the more energetic high-frequency components of the ZPE to a more easily captured form. We are discussing the possibility of a collaborative effort between us to determine whether such an approach is feasible.
Finally, an approach utilizing micro-cavity techniques to perturb the ground state stability of atomic hydrogen is under consideration in our lab. It is based on a 1987 paper of mine in which I put forth the hypothesis that the nonradiative nature of the ground state is due to a dynamic equilibrium in which radiation emitted due to accelerated electron ground state motion is compensated by absorption from the ZPE.
If this hypothesis is true, there exists the potential for energy generation by the application of the techniques of so-called cavity quantum electrodynamics QED. In cavity QED, excited atoms are passed through Casimir-like cavities whose structure suppresses electromagnetic cavity modes at the transition frequency between the atom’s excited and ground states.
The result is that the so-called “spontaneous” emission time is lengthened considerably (for example, by factors of ten), simply because spontaneous emission is not so spontaneous after all, but rather is driven by vacuum fluctuations. Eliminate the modes, and you eliminate the zero-point fluctuations of the modes, hence suppressing decay of the excited state.
As stated in an April 1993 Scientific American review article on cavity QED, “An excited atom that would ordinarily emit a low-frequency photon cannot do so, because there are no vacuum fluctuations to stimulate its emission….”
In its application to energy generation, mode suppression would be used to perturb the hypothesized dynamic ground-state absorption/emission balance to lead to energy release (patent pending).
An example in which Nature herself may have taken advantage of energetic vacuum effects is discussed in a model published by ZPE colleagues A. Rueda of California State University at Long Beach, B. Haisch of Lockheed-Martin, and D. Cole of IBM. In a paper published in the Astrophysical Journal in 1995, they propose that the vast reaches of outer space constitute an ideal environment for ZPE acceleration of nuclei and thus provide a mechanism for “powering up” cosmic rays. Details of the model would appear to account for other observed phenomena as well, such as the formation of cosmic voids.
This raises the possibility of utilizing a “sub-cosmic-ray” approach to accelerate protons in a cryogenically-cooled, collision-free vacuum trap and thus extract energy from the vacuum fluctuations by this mechanism.
THE VACUUM AS THE SOURCE OF GRAVITY AND INERTIA
What of the fundamental forces of gravity and inertia that we seek to overcome in space travel? We have phenomenological theories that describe their effects (Newton’s Laws and their relativistic generalizations), but what of their origins?
The first hint that these phenomena might themselves be traceable to roots in the underlying fluctuations of the vacuum came in a 1967 study published by the well-known Russian physicist Andrei Sakharov. Searching to derive Einstein’s phenomenological equations for general relativity from a more fundamental set of assumptions, Sakharov came to the conclusion that the entire panoply of general relativistic phenomena could be seen as induced effects brought about by changes in the quantum-fluctuation energy of the vacuum due to the presence of matter.
In this view the attractive gravitational force is more akin to the induced Casimir force discussed above, than to the fundamental inverse square law force between charged particles with which it is often compared. Although speculative when first introduced by Sakharov, this hypothesis has led to a rich and ongoing literature (including a contribution of my own in 1989) on quantum-fluctuation-induced gravity, a literature that continues to yield deep insight into the role played by vacuum forces.
Given an apparent deep connection between gravity and the zero-point fluctuations of the vacuum, a similar connection must exist between these self-same vacuum fluctuations and inertia. This is because it is an empirical fact that the gravitational and inertial masses have the same value, even though the underlying phenomena are quite disparate.
Why, for example, should a measure of the resistance of a body to being accelerated, even if far from any gravitational field, have the same value that is associated with the gravitational attraction between bodies? Indeed, if one is determined by vacuum fluctuations, so must the other.
To get to the heart of inertia, consider a specific example in which you are standing on a train in the station. As the train leaves the platform with a jolt, you could be thrown to the floor. What is this force that knocks you down, seemingly coming out of nowhere?
This phenomenon, which we conveniently label inertia and go on about our physics, is a subtle feature of the universe that has perplexed generations of physicists from Newton to Einstein. Since in this example the sudden disquieting imbalance results from acceleration “relative to the fixed stars,” in its most provocative form one could say that it was the “stars” that delivered the punch. This key feature was emphasized by the Austrian philosopher of science Ernst Mach, and is now known as Mach’s Principle. Nonetheless, the mechanism by which the stars might do this deed has eluded convincing explication.
Addressing this issue in a 1994 paper entitled “Inertia as a Zero-Point Field Lorentz Force,” Haisch, Rueda and I were successful in tracing the problem of inertia and its connection to Mach’s Principle to the ZPE properties of the vacuum.
In a sentence, although a uniformly moving body does not experience a drag force from the (Lorentz-invariant) vacuum fluctuations, an accelerated body meets a resistance (force) proportional to the acceleration.
By accelerated we mean, of course, accelerated relative to the fixed stars. It turns out that an argument can be made that the quantum fluctuations of distant matter structure the local vacuum-fluctuation frame of reference (see Puthoff, “Source…,” 1989). Thus, in the example of the train the punch was delivered by the wall of vacuum fluctuations acting as a proxy for the fixed stars through which one attempted to accelerate.
The implication for space travel is this: Given the evidence generated in the field of cavity QED (discussed above), there is experimental evidence that vacuum fluctuations can be altered by technological means. This leads to the corollary that, in principle, gravitational and inertial masses can also be altered.
The possibility of altering mass with a view to easing the energy burden of future spaceships has been seriously considered by the Advanced Concepts Office of the Propulsion Directorate of the Phillips Laboratory at Edwards Air Force Base. Gravity researcher Robert Forward accepted an assignment to review this concept. His deliverable product was to recommend a broad, multi-pronged effort involving laboratories from around the world to investigate the inertia model experimentally.
After a one-year investigation Forward finished his study and submitted his report to the Air Force, who published it under the title Mass Modification Experiment Definition Study. The Abstract reads in part:
“…. Many researchers see the vacuum as a central ingredient of 21st- Century physics. Some even believe the vacuum may be harnessed to provide a limitless supply of energy. This report summarizes an attempt to find an experiment that would test the Haisch, Rueda and Puthoff (HRP) conjecture that the mass and inertia of a body are induced effects brought about by changes in the quantum-fluctuation energy of the vacuum…. It was possible to find an experiment that might be able to prove or disprove that the inertial mass of a body can be altered by making changes in the vacuum surrounding the body.”
With regard to action items, Forward in fact recommends a ranked list of not one but four experiments to be carried out to address the ZPF-inertia concept and its broad implications. The recommendations included investigation of the proposed “sub-cosmic-ray energy device” mentioned earlier, and the investigation of an hypothesized “inertia-wind” effect proposed by our laboratory and possibly detected in early experimental work by Forward and Miller, though the latter possibility is highly speculative at this point.
ENGINEERING THE VACUUM FOR “WARP DRIVE”
Perhaps one of the most speculative, but nonetheless scientifically- grounded, proposals of all is the so-called Alcubierre Warp Drive. Taking on the challenge of determining whether Warp Drive a la Star Trek was a scientific possibility, general relativity theorist Miguel Alcubierre of the University of Wales set himself the task of determining whether faster- than-light travel was possible within the constraints of standard theory.
Although such clearly could not be the case in the flat space of special relativity, general relativity permits consideration of altered spacetime metrics where such a possibility is not a priori ruled out.
Alcubierre’s further self-imposed constraints on an acceptable solution included the requirements that no net time distortion should occur (breakfast on Earth, lunch on Alpha Centauri, and home for dinner with your wife and children, not your great-great-great grandchildren), and that the occupants of the spaceship were not to be flattened against the bulkhead by unconscionable accelerations.
A solution meeting all of the above requirements was found and published by Alcubierre in Classical and Quantum Gravity in 1994. The solution discovered by Alcubierre involved the creation of a local distortion of spacetime such that spacetime is expanded behind the spaceship, contracted ahead of it, and yields a hypersurfer-like motion faster than the speed of light as seen by observers outside the disturbed region. In essence, on the outgoing leg of its journey the spaceship is pushed away from Earth and pulled towards its distant destination by the engineered local expansion of spacetime itself.
(For follow-up on the broader aspects of “metric engineering” concepts, one can refer to a paper published by myself in Physics Essays in 1996.)
Interestingly enough, the engineering requirements rely on the generation of macroscopic, negative-energy-density, Casimir-like states in the quantum vacuum of the type discussed earlier. Unfortunately, meeting such requirements is beyond technological reach without some unforeseen breakthrough, as emphasized by Pfenning and Ford in a recently submitted manuscript.
Related, of course, is the knowledge that general relativity permits the possibility of wormholes, topological tunnels which in principle could connect distant parts of the universe, a cosmic subway so to speak.
Publishing in the American Journal of Physics in 1988, theorists Morris and Thorne initially outlined in some detail the requirements for traversible wormholes and have found that, in principle, the possibility exists provided one has access to Casimir-like, negative-energy-density quantum vacuum states. This has led to a rich literature, summarized recently in a 1996 book by Matt Visser of Washington University, St. Louis.
Again, the technological requirements appear out of reach for the foreseeable future, perhaps awaiting new techniques for cohering the ZPE vacuum fluctuations in order to meet the energy-density requirements.
CONCLUSIONS
We began this discussion with the question: “Can the vacuum be engineered for spaceflight applications?” The answer is: “In principle, yes.” However, engineering-wise it is clear that there is a long way to go. Given the cliche “a journey of 1000 miles begins with the first steps,” it is also clear that we can take those first steps now in the laboratory.
Given that Casimir and related effects indicate the possibility of tapping the enormous residual energy in the vacuum-fluctuation ZPE, and the demonstration in cavity QED that portions of the ZPE spectrum can be manipulated to produce macroscopic technological effects such as the inhibition of spontaneous emission of excited states in quantum systems, it would appear that the first steps along this path are visible.
This, combined with newly-emerging concepts of the relationship of gravity, inertia and warp drive to properties of the vacuum as a manipulable medium, indicate yet further reaches of possible technological development, although requiring yet unforeseen breakthroughs with regard to the possibility of engineering vacuum fluctuations to produce desired results.
Where does this leave us? As we peer into the heavens from the depth of our gravity well, hoping for some “magic” solution that will launch our spacefarers first to the planets and then to the stars, we are reminded of Arthur C. Clarke’s phrase that highly-advanced technology is essentially indistinguishable from magic. Fortunately, such magic appears to be waiting in the wings of our deepening understanding of the quantum vacuum in which we live.
REFERENCES
– Lee, T.D. (1988) Particle Physics and Introduction to Field Theory, Harwood Academic, London.
– Feynman, R.P., and Hibbs, A.R. (1965) Quantum Mechanics and Path Integrals, McGraw-Hill, New York.
– Forward, R.L. (1984) “Extracting electrical energy from the vacuum by cohesion of charged foliated conductors”, Phys. Rev. B, Vol. 30, No. 4, pp. 1700-1702.
– Casimir, H.G.B. (1948) “On the attraction between two perfectly conducting plates”, Proc. Kon. Ned. Akad. van Weten., Vol. 51, No. 7, pp. 793-796.
– Lamoreaux, S.K. (1997) “Demonstration of the Casimir force in the 0.6 to 6 mm range”, Phys. Rev. Lett., Vol. 78, No. 1, pp. 5-8.
– Milonni, P.W., Cook, R.J., and Goggin, M.E. (1988) “Radiation pressure from the vacuum: Physical interpretation of the Casimir force”, Phys. Rev. A, Vol. 38, No. 3, pp. 1621-1623.
– Cole, D.C., and Puthoff, H.E. (1993) “Extracting energy and heat from the vacuum”, Phys. Rev. E, Vol. 48, No. 2, pp. 1562-1565.
– Puthoff, H.E. (1990) “The energetic vacuum: Implications for energy research”, Spec. in Sci. and Tech., Vol. 13, No. 4, pp. 247-257.
– Puthoff, H.E., and Piestrup, M.A. (1997) “On the possibility of charge confinement by van der Waals/Casimir-type forces”, subm. to Phys. Lett. B.
– Shoulders, K.R. (1991) “Energy conversion using high charge density”, U.S. Patent No. 5,018,180, issued May 21, 1991.
– Schwinger, J. (1993) “Casimir light: The source”, Proc. Natl. Acad. Sci., Vol. 90, pp. 2105-2106.
– George, D.R., and Stringham, R.S. (1996) “Technical report on the demonstration of new technology producing heat and nuclear products via cavitation induced micro-fusion in the E-Quest Sciences Mark II research device”, EPRI Project Final Report, Work Order #3170-28, Palo Alto, CA, May 1996.
– Mead, Jr., F.B., and Nachamkin, J. (1996) “System for converting electromagnetic radiation energy to electrical energy”, U.S. Patent No. 5,590,031, issued Dec. 31, 1996.
– Puthoff, H.E. (1987) “Ground state of hydrogen as a zero-point-fluctuation- determined state”, Phys. Rev. D, Vol. 35, No. 10, pp. 3266-3269.
– Haroche, S, and Raimond, J.-M. (1993) “Cavity quantum electrodynamics”, Sci. Am., April 1993, pp. 54-62.
– Rueda, A., Haisch, B. and Cole, D.C. (1995) “Vacuum zero-point field pressure instability in astrophysical plasmas and the formation of cosmic voids”, Astrophys. J., Vol. 445, pp. 7-16.
– Sakharov, A. (1968) “Vacuum quantum fluctuations in curved space and the theory of gravitation”, Sov. Phys.-Dokl., Vol. 12, No. 11, pp. 1040-1041.
– Puthoff, H.E. (1989, 1993) “Gravity as a zero-point-fluctuation force”, Phys. Rev. A, Vol. 39, No. 5, pp. 2333-2342; Vol. 47, No. 4, pp. 3454-3455.
– Haisch, B., Rueda, A., and Puthoff, H.E. (1994) “Inertia as a zero point field Lorentz force”, Phys. Rev. A, Vol. 49, No. 2, pp. 679-694.
– Puthoff, H. E. (1989, 1991) “Source of vacuum electromagnetic zero-point energy”, Phys. Rev. A, Vol. 40, No. 9, pp. 4857-4862; Vol. 44, No. 5, pp. 3385-3386.
– Forward, R.L. (1996) “Mass modification experiment definition study”, J. Sci. Exploration, Vol. 10, No. 3, pp. 325-354.
– Forward, R.L., and Miller, L.R. (1967) “Generation and detection of dynamic gravitational-gradient fields”, J. Appl. Phys., Vol. 38, No. 2, pp. 512- 518.
– Alcubierre, M. (1994) “The warp drive: Hyper-fast travel within general relativity”, Class. Quant. Grav., Vol. 11, pp. L73-L77.
– Puthoff, H.E. (1996) “SETI, the velocity-of-light limitation, and the Alcubierre warp drive: An integrating overview”, Phys. Essays, Vol. 9, No. 1, pp. 156-158.
– Pfenning, M.J., and Ford, L.H. (1997) “The unphysical nature of ‘warp drive'”, subm. to Class. Quant. Grav.
– Morris, M., and Thorne, K.S. (1988) “Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity”, Am. J. Phys., Vol. 56, No. 5, pp. 395-412.
– Visser, M. (1996) Lorentzian Wormholes, AIP Press, Woodbury, NY.
# Engineering the Zero Point Field and Polarizable Vacuum for Interstellar Flight – KeelyNet 04/06/02 – http://www.keelynet.com/energy/engzpf.htm
Introduction
A paper that I presented at the First International Workshop on Field Propulsion in the UK a little over a year ago has now been published (after peer review and changes) in the Journal of the British Interplanetary Society (JBIS), copy enclosed. We are very pleased with this publication, as it presents a very balanced view.
First, we cover the potential promise of manipulating vacuum energy for spaceflight energy/propulsion, while also presenting a very sober analysis of the daunting problems involved.
Second, we take a look at the so-called EXH electromagnetic field propulsion of interest to many, only to find (unfortunately) that it is flawed at its roots because of rather arcane reasons. Hopefully this latter finding will encourage other researchers to redirect their efforts along more fruitful lines.
Finally, in Table 2 we present the basics of truly exotic propulsion based on a metric engineering approach to general relativity that hopefully some day will result in engineering embodiments.
Best regards, feel free to post it. All I have is the pdf.
Cheers, Hal
– See transcription below or download from : Engineering the Zero Point Field http://www.keelynet.com/energy/engzpf.pdf
# Engineering the Zero Point Field and Polarizable Vacuum for Interstellar Flight, H.E. PUTHOFF, S.R. LITTLE and M. IBISON, from JBIS, Vol. 55, pp. 137-144, 2002
A theme that has come to the fore in advanced planning for long-range space exploration is the concept of ‘propellantless propulsion’ or ‘field propulsion’. One version of this concept involves the projected possibility that empty space itself (the quantum vacuum, or space-time metric) might be manipulated so as to provide energy/thrust for future space vehicles[1]. Although far reaching, such a proposal is solidly grounded in modern theory that describes the vacuum as a polarizable medium that sustains energetic quantum fluctuations. Thus the possibility that matter/vacuum interactions might be engineered for space-flight applications is not a priori ruled out, although certain constraints need to be acknowledged. The structure and implications of such a far reaching hypothesis are considerable herein.
Keywords: Zero-point energy, warp drive, propellantless propulsion, metric emgineering, interstellar flight.
1 – Introduction
The concept of ‘engineering the vacuum’ found its first expression in the mainstream physics literature when it was introduced by T.D. Lee in his textbook Particle Physics and Introduction to Field Theory [2]. There he stated” ‘The experimental method to alter the properties of the vacuum may be called vacuum engineering … If indeed we are able to alter the vacuum, then we may encounter some new phenomena, totally unexpected’. This legitimization of the vacuum engineering concept was based on the recognition that the vacuum is chracterized by parameters and structure that leave no doubt that it constitutes an energetic medium in its own right. Foremost among these are its properties that (1) within the context of quantum theory the vacuum is the seat of energetic particule and field fluctuations, and (2) within the contaxt of general relativity the vacuum is the seat of a space-time structure (metric) that encodes the distribution of matter and energy. Indeed, on the flyleaf of a book of essays by Einstein and others on the properties of the vacuum we find the statement ‘The vacuum is fast emerging as the central structure of modern physics’ [3].
Given the known characteristics of the vacuum, one might reasonably inquire as to why it is not immediately obvious how to catalyze robust interactions of the type sought for space-flight applications. To begin, in the case of quantum fluctuations there are uncertainties that remain to be clarified regarding global thermodynamic and energy constraints. Furthermore, the energetic components of potential utility involve very small-wavelength, high-frequency fields and thus resist facile engineering solutions. With regard to perturbation of the space-time metric, the required energy densities exceed by many orders of magnitude values achievable with existing engineering techniques. Nonetheless, we can examine the constraints, possibilities and implications under the expectation that as technology matures, felicitous means may be found that permit the exploitation of the enormous, as-yet-untapped potential of so-called ’empty space’.
2 – Propellantless Propulsion
2.1 Global Constraint
Regardless of the mechanisms that might be entertained with regard to ìpropellantlessî or ìfieldî propulsion of a spaceship, there exist certain constraints that can be easily overlooked but must be taken into consideration. A central one is that, because of the law of conservation of momentum, the center of mass-energy (CM) of an initially stationary isolated system cannot change its position if not acted upon by outside forces. This means that propellantless or field propulsion, whatever form it takes, is constrained to involve coupling to the external universe in such a way that the displacement of the CM of the spaceship is matched by a counteracting effect in the universe to which it is coupled, so as not to violate the global CM constraint.
Therefore, before one launches into a detailed investigation of a proposed propulsion mechanism it is instructive to apply this principle as an overall constraint to determine whether the principle is violated. Surprising subtleties may be involved in such an assessment, as illustrated in the following example.
2.2 An Example: ExH – Electromagnetic Field Propulsion
A recurring theme in electromagnetic propulsion considerations is that one might employ crossed electric and magnetic fields to generate propulsive force, what we might call ExH propulsion. The idea is based on the fact that propagating electromagnetic fields (photons) possess momentum carried by the crossed (orthogonal) E and H fields (Poynting vector). This raises the issue as to whether static (i.e., non-propagating) ExH fields also constitute momentum (as the mathematics would imply), and in particular whether changes in static fields could result in the transfer of momentum to an attached structure. As it turns out, the answer can be yes, as illustrated in the example of the Feynman disk paradox [4]. Electric charge distributed around the rim of a non-rotating disk generates a static electric field that extends outward from the rim, and a current-carrying coil of wire mounted perpendicular to the plane of the disk generates a static dipole magnetic field. The two fields result in a static ExH distribution that encircles the disk. Even though nothing is apparently in motion, if we take the ExH momentum concept seriously it would appear that there is angular momentum ‘circulating’ about the disk in the static fields. That this is in fact the case is demonstrated by the fact that when the current in the coil is interrupted, thereby extinguishing the magnetic field component of the ExH distribution, the disk begins to rotate. This behaviour supports the notion that, indeed, the static fields do contain angular momentum that is then transferred to the disk (to conserve angular momentum) when the field momentum is extinguished [5]. This leads one to wonder if the same principle could be applied to generate linear thrust by changes in static ExH fields, properly arrayed.
Pursuit of the linear thrust possibility, however, leads one to a rich literature concerning so-called ‘hidden momentum’ that, perhaps surprisingly, denies this possibility [6]. The ìhidden momentumî phrase refers to the fact that although the linear ExH fields do carry momentum as in the angular case, the symmetry conditions for the linear case are such that there exists a cancelling mechanical momentum contained in the structures even though a structures CM itself is stationary (see Appendix A).
Specifically, it can be shown on very general grounds that, contrary to the case for angular momentum (e.g., the Feynman disk), the total linear momentum of any stationary distribution of matter, charge and their currents, and their associated fields, must vanish.
In other words, barring a new discovery that modifies the present laws of physics, any such distribution cannot generate a propulsive force without emitting some form of reaction mass or energy, or otherwise imparting momentum to another system [7].
3. The Quantum Vacuum
3.1 Zero-Point Energy (ZPE) Background
Quantum theory tells us that so-called ’empty space’ is not truly empty, but is the seat of myriad energetic quantum processes. Specifically, quantum field theory tells us that, even in empty space, fields (e.g., the electromagnetic field) continuously fluctuate about their zero baseline values. The energy associated with these fluctuations is called zeropoint energy (ZPE), reflecting the fact that such activity remains even at a temperature of absolute zero. Such a concept is almost certain to have profound implications for future space travel, as we will now discuss.
When a hypothetical ZPE-powered spaceship strains against gravity and inertia, there are three elements of the equation that the ZPE technology could in principle address: (1) a decoupling from gravity, (2) a reduction of inertia, or (3) the generation of energy to overcome both.
3.2 Gravity
With regard to a ZPE basis for gravity, the Russian physicist Andrei Sakharov was the first to propose that in a certain sense gravitation is not a fundamental interaction at all, but rather an induced effect brought about by changes in the quantum-fluctuation energy of the vacuum when matter is present [8]. In this view, the attractive gravitational force is more akin to the induced van der Waals and Casimir forces, than to the fundamental Coulomb force. Although quite speculative when first introduced by Sakharov in 1967, this hypothesis has led to a rich literature on quantum-fluctuation-induced gravity. (The latter includes an attempt by one of the authors to flesh out the details of the Sakharov proposal [9], though difficulties remain [10]). Given the possibility of a deep connection between gravity and the zero-point fluctuations of the vacuum, it would therefore appear that a potential route to gravity decoupling would be via control of vacuum fluctuations.
3.3 Inertia
Closely related to the ZPE basis for gravity is the possibility of a ZPE basis for inertia. This is not surprising, given the empirical fact that gravitational and inertial masses have the same value, even though the underlying phenomena are quite disparate; one is associated with the gravitational attraction between bodies, while the other is a measure of resistance to acceleration, even far from a gravitational field. Addressing this issue, the author and his colleagues evolved a ZPE model for inertia which developed the concept that although a uniformly moving body does not experience a drag force from the (Lorentz-invariant) vacuum fluctuations, an accelerated body meets a resistive force proportional to the acceleration [11], an approach that has had a favourable reception in the scientific community [12]. Again, as in the gravity case, it would therefore appear that a potential route to the reduction of inertial mass would be via control of vacuum fluctuations.
Investigation into this possibility by the U.S. Air Force’s Advanced Concepts Office at Edwards Air Force Base resulted in the generation of a report entitled Mass Modification Experiment Definition Study that addressed just this issue [13]. Included in its recommendations was a call for precision measurement of what is called the Casimir force. The Casimir force is an attractive quantum force between closely spaced metal or dielectric plates (or other structures) that derives from partial shielding of the interior region from the background zeropoint fluctuations of the vacuum electromagnetic field, which results in unbalanced ZPE radiation pressures [14]. Since issuance of the report, such precision measurements have been made which confirm the Casimir effect to high accuracy [15], measurements which even attracted high-profile attention in the media [16]. The relevance of the Casimir effect to our considerations is that it constitutes experimental evidence that vacuum fluctuations can be altered by technological means. This suggests the possibility that, given the models discussed, gravitational and inertial masses might also be amenable to modification. The control of vacuum fluctuations by the use of cavity structures has already found practical application in the field of cavity quantum electrodynamics, where the spontaneous emission rates of atoms are subject to manipulation [17].
Therefore, it is not unreasonable to contemplate the possibility of such control in the field of space propulsion.
3.4 Energy Extraction
With regard to the extraction of energy from the vacuum fluctuation energy reservoir, there are no energetic or thermodynamic constraints preventing such release under certain conditions [18]. And, in fact, there are analyses in the literature that suggest that such mechanisms are already operative in Nature in the ìpowering upî of cosmic rays [19], or as the source of energy release from supernovas [20] and gamma-ray bursts [21].
For our purposes, the question is whether the ZPE can be ‘mined’ at a level practical for use in space propulsion. Given that the ZPE energy density is conservatively estimated to be on the order of nuclear energy densities or greater [22], it would constitute a seemingly ubiquitous energy supply, a veritable ‘Holy Grail’ energy source.
One of the first researchers to call attention to the principle of the use of the Casimir effect as a potential energy source was Robert Forward at Hughes Research Laboratories in Malibu, CA [23].
Though providing ‘proof-of-principle,’ unlike the astrophysical implications cited above the amount of energy release for mechanical structures under laboratory conditions is minuscule. (The collapse of a pair of one-centimeter-square Casimir plates from, say, 2 microns to 1 micron in 1 microsecond, generates around 1/10 microwatt.) In addition, the conservative nature of the Casimir effect would appear to prevent recycling, though there have been some suggestions for getting around this barrier [24]. Alternatives involving non-recycling behaviour, such as plasma pinches [25] or bubble collapse in sonoluminescence [26], have been investigated in our laboratory and elsewhere, but as yet without real promise for energy applications.
Vacuum energy extraction approaches by other than the Casimir effect are also being considered.
One approach that emerged from the Air Force’s Mass Modification study [13] was the suggestion that the ZPE-driven cosmic ray model be explored under laboratory conditions to determine whether protons could be accelerated by the proposed cosmic ray mechanism in a cryogenically-cooled, collision-free vacuum trap. Yet another proposal (for which a patent has been issued) is based on the concept of beat-frequency downshifting of the more energetic high-frequency components of the ZPE, by use of slightly detuned dielectric-sphere antennas [27].
In our own laboratory we have considered an approach based on perturbation of atomic or molecular ground states, hypothesized to be equilibrium states involving dynamic radiation/absorption exchange with the vacuum fluctuations [28]. In this model atoms or molecules in a ZPE-limiting Casimir cavity are expected to undergo energy shifts that would alter the spectroscopic signatures of excitations involving the ground state. We have initiated experiments at a synchrotron facility to explore this ZPE/ground-state relationship, though so far without success. In addition to carrying out experiments based on our own ideas, our laboratory also acts as a clearing-house to evaluate the experimental concepts and devices of others who are working along similar lines. Details can be found on our website, www.earthtech.org.
Whether tapping the ZPE as an energy source or manipulating the ZPE for gravity/inertia control are but gleams in a spaceship designerís eye, or a Royal Road to practical space propulsion, is yet to be determined. Only by explorations of the type described here will the answer emerge. In the interim a quote by the Russian science historian Roman Podolny would seem to apply: ìIt would be just as presumptuous to deny the feasibility of useful application as it would be irresponsible to guarantee such applicationî [29].
4. The Space-Time Metric(‘Metric Engineering’Approach)
Despite the apparently daunting energy requirements to perturb the space-time metric to a significant degree, we examine the structure that such perturbations would take under conditions useful for space-flight application, a ‘Blue Sky’ approach, as it were.
Although topics in general relativity are routinely treated in terms of tensor formulations in curved space-time, we shall find it convenient for our purposes to utilize one of the alternative methodologies for treating metric changes that has emerged over the years in studies of gravitational theories.
The approach, known as the polarizable vacuum (PV) representation of general relativity (GR), treats the vacuum as a polarizable medium [30]. The PV approach treats metric changes in terms of the permittivity and permeability constants of the vacuum, eo and µo, essentially along the lines of the ‘TH eµ’ methodology used in comparative studies of gravitational theories [31]. Such an approach, relying as it does on parameters familiar to engineers, can be considered a ìmetric engineeringî approach.
In brief, Maxwellís equations in curved space are treated in the isomorphism of a polarizable medium of variable refractive index in flat space [32]; the bending of a light ray near a massive body is modelled as due to an induced spatial variation in the refractive index of the vacuum near the body; the reduction in the velocity of light in a gravitational potential is represented by an effective increase in the refractive index of the vacuum, and so forth. As elaborated in Ref. 30 and the references therein, though differing in some aspects from GR, PV modelling can be carried out for cases of interest in a self-consistent way so as to reproduce to appropriate order both the equations of GR, and the match to the classical experimental tests of those equations.
Specifically, the PV approach treats such measures as the velocity of light, the length of rulers (atomic bond lengths), the frequency of clocks, particle masses, and so forth, in terms of a variable vacuum dielectric constant K in which vacuum permittivity eo transforms to eo –> K eo, vacuum permeability to µo –> K µo. In a planetary or solar gravitational potential K inf.1 + 2GM/ rc2 , and the results are as shown in Table 1. Thus, the velocity of light is reduced, light emitted from an atom is redshifted as compared with an atom at infinity (K = 1), rulers shrink, etc.
As one example of the significance of the tabulated values, the dependence of fundamental length measures (ruler shrinkage) on the variable K indicates that the dimensions of material objects adjust in accordance with local changes in vacuum polarizability – thus there is no such thing as a perfectly rigid rod. From the standpoint of the PV approach this is the genesis of the variable metric that is of such significance in GR studies. It also permits us to define, from the viewpoint of the PV approach, just what precisely is meant by the label ìcurved space.î In the vicinity of, say, a planet or star, where K>1, if one were to take a ruler and measure along a radius vector R to some circular orbit, and then measure the circumference C of that orbit, one would obtain C
This is a consequence of the ruler being relatively shorter during the radial measuring process when closer to the body where K is relatively greater, as compared to its length during the circumferential measuring process when further from the body. Such an influence on the measuring process due to induced polarizability changes in the vacuum near the body leads to the GR concept that the presence of the body ìinfluences the metric,î and correctly so.
We are now in a position to consider application of this ‘metric engineering’ formalism to the type of questions relevant to space propulsion.
As we show in Appendix B, under certain conditions the metric can in principle be modified to reduce the value of the vacuum dielectric constant K to below unity. Returning to Table 1, we see that a K 
Under such conditions of extreme space-time perturbation, the local velocity of light (as seen from a reference frame at infinity) is increased, mass decreases, energy bond strengths increase, etc., features presumably attractive for interstellar travel.
As an example, one specific approach that has generated considerable commentary in the technical literature is the so-called Alcubierre Warp Drive, named after its creator, general relativity theorist Miguel Alcubierre [33, 34]. Alcubierre showed that by distorting the local space-time metric in the region of a spaceship in a certain prescribed way, it would be possible in principle to achieve motion faster than the speed of light as judged by observers outside the disturbed region, without violating the local velocity-of-light constraint within the region.
Furthermore, the Alcubierre solution showed that the proper (experienced) acceleration along the spaceshipís path would be zero, and that the spaceship would suffer no time dilation, highly desirable features for interstellar travel.
When it comes to engineering the Alcubierre solution, however, seemingly insurmountable obstacles emerge. For a 100 m warp bubble the bubble wall thickness approaches a Planck length (~10-35 m) and the (negative) energy required is roughly 10 orders of magnitude greater than the total mass of the universe! [35] Further theoretical effort has resulted in a reduction of the energy requirement to somewhat below a solar mass, an impressive advance but still quite impractical [36].
Analysis of related alternatives such as the Krasnikov Tube [37] and traversable wormholes have fared no better [38]. Thus, if success is to be achieved, it must rest on some as yet unforeseen breakthrough about which we can only speculate, such as a technology to cohere otherwise random vacuum fluctuation energy.
Clearly then, calculations for the proposed geometries are by no means directly applicable to the design of a space propulsion drive. However, these sample calculations indicate the direction of potentially useful trends derivable on the basis of the application of GR principles as embodied in a metric engineering approach, with the results constrained only by what is achievable practically in an engineering sense. The latter is, however, a daunting constraint.
5. Conclusions
In this paper we have touched briefly on innovative forms of space propulsion, especially those that might exploit properties of the quantum vacuum or the space-time metric in a fundamental way. At this point in the development of such nascent concepts it is premature to even guess at an optimum strategy, let alone attempt to forge a critical path; in fact, it remains to be determined whether such exploitation is even feasible. Nonetheless, only by inquiring into such concepts in a rigorous way can we hope to arrive at a proper assessment of the possibilities and thereby determine the best course of action to pursue in our steps first to explore our solar system environment, and then one day to reach the stars.
Appendix A – Hidden Momentum
Consider a stationary current loop which consists of an incompressible fluid of positive charge density p circulating at velocity v clockwise around a loop of non-conductive piping of cross sectional area a. The loop is immersed in a constant uniform electric field E.
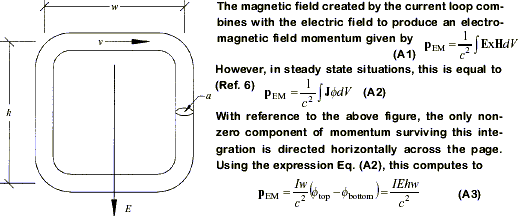
where the sense is from left to right. From this it is concluded that there is a steady net linear momentum stored in the electromagnetic fields. We will now show there is another momentum, equal and opposite to this electromagnetic field momentum.
Since the current flowing in the loop is given by I = pav, the velocity of the fluid is everywhere v = I/ pa. Meanwhile, the external electric field E creates a pressure difference between the bottom and the top of the fluid given by P = pEh. Moving to the left, therefore, is a net energy flux S (energy per unit area per unit time) given by
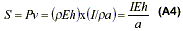
But since energy has mass, Eq. (A4) may be converted to an expression for momentum. This is mostly easily accomplished by writing the Einstein relation E = mc2 in flux density form as S = gc2, where g is the momentum per unit volume. It now follows that, due to the different pressures at the top and bottom of the loop, there must be a net overall momentum – directed to the left – given by
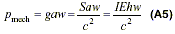
where the subscript ‘mech’ draws attention to the apparently entirely mechanical origin of this momentum.
Eqs. (A5) and (A3) demonstrate that the electromagnetic momentum is balanced by an equal and opposite mechanical momentum. Because of its rather obscure nature, this momentum has been referred to in the literature as ‘hidden momentum’.
This is a particular example of the general result that a net static linear field momentum will always be balanced by an equal and opposite hidden mechanical momentum. In practical terms, this means that the creation of linear field momentum cannot give rise to motion because the field momentum is automatically neutralized by a mechanical momentum hidden within the structure, so that the whole system remains stationary.
This inability to utilize linear field momentum for propulsion is guaranteed by the law of momentum conservation.
Appendix B – Metric Engineering Solutions
In the polarizable vacuum (PV) approach the equation that plays the role of the Einstein equation (curvature driven by the mass-energy stress tensor) for a single massive particle at the origin is (Ref. 30)

The solution that satisfies the Newtonian limit is given by
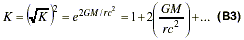
which can be shown to reproduce to appropriate order the standard GR Schwarzschild metric properties as they apply to the weak-field conditions prevailing in the solar system.
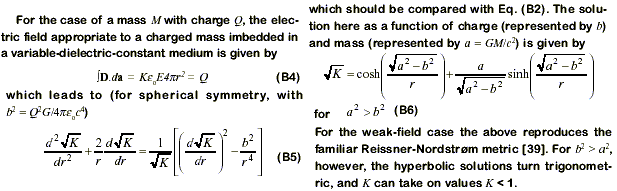
References
– 1. H.E. Puthoff, ‘ Can the vacuum be engineered for spaceflight applications? Overview of theory andexperiments ‘, Jour. Sci. Exploration, 12, p.295, 1998.
See also H.E. Puthoff, ‘ Space propulsion: Can empty space itself provide a solution? ‘ , Ad Astra, 9, (National Space Society), p.42, Jan/Feb 1997.
– 2. T.D. Lee, Particle Physics and Introduction to Field Theory ,Harwood Academic Press, London, 1988.
– 3. S. Saunders and H. R. Brown, ” The Philosophy of Vacuum , Eds., Clarendon Press, Oxford, 1991.
– 4. R.P. Feynman, R.B. Leighton and M. Sands, The Feynman Lectures on Physics , Addison-Wesley, Reading, MA, Vol. II, p.17-5, 1964.
– 5. For experimental confirmation see, for example, G.M. Graham and D.G. Lahoz, ‘ Observation of static electromagnetic angular momentum in vacuo ‘, Nature, 285, p.154, 1980.
– 6. V. Hnizdo, ‘ Hidden momentum of a relativistic fluid carrying current in an external electric field ‘, Am. J. Phys., 65, p.92, 1997.
– 7. Proposals to push directly against the space-time metric or quantum vacuum, i.e., use the rest of the Universe as a springboard by means presently unknown, fall into the latter category.
– 8. A.D. Sakharov, ‘ Vacuum quantum fluctuations in curved space and the theory of gravitation ‘, Dokl. Akad. Nauk SSSR, [Sov. Phys. – Dokl. 12, p.1040, 1968].
See also C. W. Misner, K. S. Thorne and J. A. Wheeler, Gravitation , Freeman, San Francisco, pp.426-428,1973.
– 9. H.E. Puthoff, ‘ Gravity as a zero-point-fluctuation force ‘, Phys. Rev. A, 39, p.2333, 1989.
– 10. H.E. Puthoff, ‘ Reply to Comment on Gravity as a zero-point-fluctuation force ‘, Phys. Rev. A, 47, p.3454, 1993.
– 11. B. Haisch, A. Rueda and H.E. Puthoff, ‘ Inertia as a zero-point field Lorentz force ‘, Phys. Rev. A, 49, p.678, 1994;
A. Rueda and B. Haisch, ‘ Inertia as reaction of the vacuum to accelerated motion ‘, Phys. Lett. A, 240, p.115, 1998.
– 12. M. Jammer, Concepts of Mass in Contemporary Physics and Philosophy , Princeton University Press, Princeton, pp.163-167, 2000.
– 13. R.L. Forward, ‘ Mass modification experiment definition study, ‘ Phillips Laboratory Report PL-TR-96-3004, Air Force Materiel Command, Edwards AFB, CA 93524-5000 (Feb 1996). Reprinted in Jour. Sci. Exploration, 10, p.325, 1996.
– 14. P.W. Milonni, R.J. Cook and M.E. Goggin, ‘ Radiation pressure from the vacuum: Physical interpretation of the Casimir force ‘, Phys. Rev. A, 38, p.1621, 1988.
– 15. S.K. Lamoreaux, ‘ Demonstration of the Casimir force in the 0.6 to 6 mm range ‘, Phys. Rev. Lett., 78, p.5, 1997;
U. Mohideen and A. Roy, ‘ Precision measurement of the Casimir force from 0.1 to 0.9 mm ‘, Phys. Rev. Lett., 81, p.4549, 1998.
– 16. M.W. Browne, ‘ Physicists confirm power of nothing, measuring force of quantum foam ‘, New York Times, p.C1, 21 January 1997.
– 17. See, e.g., S. Haroche and J.-M. Raimond, ‘ Cavity quantum electrodynamics ‘, Sci. Am., p.54, April 1993.
– 18. D.C. Cole and H.E. Puthoff, ‘ Extracting energy and heat from the vacuum ‘, Phys. Rev. E., 48, p.1562, 1993.
– 19. A. Rueda, B. Haisch and D.C. Cole, ‘ Vacuum zero-point field pressure instability in astrophysical plasmas and the formation of cosmic voids ‘, Astrophys. J., 445, p.7, 1995.
– 20. I.Tu. Sokolov, ‘ The Casimir effect as a possible source of cosmic energy ‘, Phys. Lett. A, 223, p.163, 1996.
– 21. C.E. Carlson, T. Goldman and J. Peres-Mercader, ‘ Gamma-ray bursts, neutron star quakes, and the Casimir effect ‘, Europhys. Lett., 36, p.637, 1996.
– 22. R.P. Feynman and A.R. Hibbs, ‘ Quantum Mechanics and Path Integrals ‘, McGraw-Hill, New York, 1965.
– 23. R.L. Forward, ‘ Extracting electrical energy from the vacuum by cohesion of charged foliated conductors ‘, Phys. Rev. B, 30, p.1700, 1984.
– 24. F. Pinto, ‘ Engine cycle of an optically controlled vacuum energy transducer ‘, Phys. Rev. B, 60, p.14740, 1999.
– 25. H.E. Puthoff, ‘ The energetic vacuum: implications for energy research ‘, Spec. in Sci. and Tech., 13, p.247, 1990;
K.R. Shoulders, ‘ Method and apparatus for production and manipulation of high density charge ‘, U.S. Patent No. 5,054,046, 1991.
– 26. J. Schwinger, ‘ Casimir light: the source ‘, Proc. Natl Acad. Sci., 90, p.2105, 1993;
C. Eberlein, ‘ Sonoluminescence as quantum vacuum radiation ‘, Phys. Rev. Lett., 76, p.3842, 1996.
– 27. F.B. Mead and J. Nachamkin, ‘ System for converting electromagnetic radiation energy to electrical energy ‘, U.S. Patent No. 5,590,031, 1996.
– 28. H.E. Puthoff, ‘ Ground state of hydrogen as a zero-pointfluctuation-determined state ‘, Phys. Rev. D, 35, p.3266, 1987.
– 29. R. Podolny, Something Called Nothing – Physical Vacuum: What is It? , Mir Publishers, Moscow, 1986.
– 30. H.E. Puthoff, ‘ Polarizable-vacuum approach to general relativity, ‘ in Gravitation and Cosmology: From the Hubble Radius to the Planck Scale , Eds. R. L. Amoroso, G. Hunter, M. Kafatos, and J.-P. Vigier, Kluwer Academic Press, Dordrecht, the Netherlands, in press, 2001.
See also H.E. Puthoff, ‘ Polarizable-vacuum (PV) representation of general relativity, ‘ http://xxx.lanl.gov/abs/gr-qc/ 9909037.
– 31. A.P. Lightman and D.L. Lee, ‘ Restricted proof that the weak equivalence principle implies the Einstein equivalence principle ‘, Phys. Rev. D, 8, p.364, 1973.
– 32. A.M. Volkov, A.A. Izmestíev and G.V. Skrotskii, ‘ The propagation of electromagnetic waves in a Riemannian space ‘, Sov. Phys. JETP, 32, p.686, 1971.
– 33. M. Alcubierre, ‘ The warp drive: Hyper-fast travel within general relativity ‘, Class. Quant. Grav., 11, L73, 1994.
– 34. H.E. Puthoff, ‘SETI, the velocity-of-light limitation, and the Alcubierre warp drive: An integrating overview ‘, Phys. Essays, 9, p.156, 1996.
– 35. M.J. Pfenning and L.H. Ford, ‘ The unphysical nature of warp drive ‘, Class. Quant. Grav., 14, p.1743, 1997.
– 36. C. Van Den Broeck, ‘ A ‘warp drive’ with more reasonable total energy requirements ‘, Class. Quant. Grav., 16, p.3973, 1999.
– 37. A.E. Everett and T.A. Roman, ‘ A superluminal subway: The Krasnikov Tube ‘, Phys. Rev. D, 56, p.2100, 1997.
– 38. M. Visser, Lorentzian Wormholes: From Einstein to Hawking , AIP Press, Woodbury, New York, 1996.
– 39. C.W. Misner, K.S. Thorne, and J.A. Wheeler, Gravitation , Freeman, San Francisco, 1973, p. 841.
(Received 2 August 2001)