## TWO-SLIT EXPERIMENT from The Tom BeardenWebsite http://www.cheniere.org/books/excalibur/2slit.htm
This experiment is fundamental to all of modern physics. Feynman, Nobel prize winner in physics, has stated that no physicist understands this experiment, and that it cannot be explained by any classical means. The reason is that it cannot be monocularly comprehended, i.e., the first three laws of logic cannot explain it. The fourth law can and does.
In the experiment, electrons are emitted from a source and travel past a doubly-slit wall region on their way to a screen. The apparatus is shielded against light. If one believes that the emitted electron is a little three-dimensional particle, much like a tiny baseball, then it should go through one of the slits and not the other. It would then hit the screen at one of the two spots indicated as the expected distribution, with a little scatter from those that chip the edge of the slit a bit. Electrons which do not hit the holes but strike the wall are absorbed.
We do not get this expected pattern. Instead, the pattern is essentially the same as the one we would get if each electron were a wavefront passing through both slits at once. However, each electron still strikes the screen in only one point; the distribution of these points fits the actual distribution pattern shown.
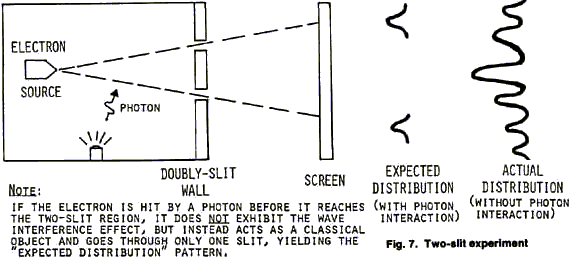
This stunned the physicists. They did not believe it at first, so they set up a photon gun and hit every electron with a photon as it left the emitter source and started over toward the two-slit region. That is, they determined precisely when a little electron was on the way, and the fact that it was like a tiny baseball and in just one place. And this time the electron only went through a single slit, and it gave the expected pattern after all. And when the experiment was repeated and only a fraction of the electrons were hit with photons, then a mixture of the two patterns emerged.
It is simple to describe the results mathematically, but no one has understood why things happen as they do in this experiment. The principle of complementarity evades the issue. This principle is simply a monocular statement dealing with one aspect of the problem at a time, with the determined, exclusive, monocular past only. It does not apply to the present or to the future. If we think in terms of the present, then the third law of logic is violated and the fourth law applies. The two states, two-dimensional wave and three-dimensional corpuscular, both exist simultaneously but nonexclusively in the present. Thus in physics terms, the entity becomes nonobjective (nonspatial), probabilistic and undetermined, and this is automatically a wave concept, i.e., since waves are not confined to one place and determined or localized, they may exist in the nonconfined, non localized present.
Note that photon interaction must be excluded whenever the so-called quantum effect is exhibited. If photon interaction is invoked, classical reality emerges. Photon interaction creates classical objectivity. Photon interaction is a time-differentiating operator imposed on L3T four-space. Specifically, since light carries time, photon emission from an entity strips away T from the L3T nonobjective entity, converting it to an L3 or spatial object.
The very concept of an object comes from primitive perception’s one-to-one correspondence with photon interaction. After photon interaction, the first three laws of logic apply to an entity. Before photon interaction occurs, the fourth law applies. In the fourth-law state, the time portion of an entity can interact with any number of time portions of other fourth-law entities if the time aspects of all of them coincide.
A free electron born and released at the emitter is four-dimensional ( L3T) until it is struck by a photon, after which it is three-dimensional (L3 ). When the wavelength of electron and slits is specified, we have actually specified the time interval stripped out of a ?E?T quantum in each quantum of fundamental change occurring. Perfect time synchronization accomplishes or constitutes orthogonal rotation. So if the length (width) dimension of each slit is very close to the wavelength of the electron, the time aspects of both slits will interact with the time aspect of the fourth-state electron if all three are brought into time phase simultaneously. If the slits are made much larger, this interaction will not occur.
When the electron interacts with both slits timewise, this will constitute a part of the past history of the electron to all future interactions or interaction possibilities. But since the interaction with the two-slits was not in the past (i.e., selected or determined), then that interaction itself is a part of the present and future probabilities chain. In physics, probabilities propagate forward in time with absolute causality until a monocular selection is made. Thus the fourth-law interaction is propagated forward with absolute causality and significantly affects any future interactions. And apparently vice-versa. John Wheeler has just shown that, in at least one sense, whether or not the emitted particle in the two-slit experiment has interacted with one or both slits can be selected after it has occurred. As is well known, the pattern of projection forward of this fourth-law interaction may be quite simply calculated from ordinary trigonometry. For an excellent discussion of the two-slit experiment, see Richard P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics. Vol. I (Addison-Wesley, Menlo Park, Calif., 1963), pp. 37 -1 and 37 -12.
When the electron hits the screen, it encounters a region of varying time oscillations of the orbital electrons around the individual atoms comprising the screen.
Thus the exact location of the orbital electron in the screen which will first precisely time-synchronize with the electron wavelength approaching the screen in four-law form will vary. Thus the place where the electron hits the screen is variably selected along the screen. The time distribution pattern of the approaching electron is recovered when the time distribution of the number of electron hits per screen length is plotted.
So one can build gadgets to cause four-law entities to multiply and interact simultaneously in time, even though the entities are normally thought of as being in different spatial locations when in the three-law state. And one can deliberately select the type of interaction to occur, four-law or three-law, simply by controlling photon interaction. The two-slit apparatus itself is a paranormal, psychotronic de vice.
This is the explanation of the two-slit experiment, which, according to Nobel prizewinner Richard Feynman, no one understands and which, according also to Dr. Feynman, contains the total mystery of quantum mechanics and the only mystery of quantum mechanics. The reason the two-slit experiment has not been understood is that the answer to the paradox was not present in the first three laws of logic. It requires the addition of the fourth law to explain the experiment.
And all fundamental particles – photons, neutrons, protons, electrons, etc. – exhibit the same behavior. So things, nothings if you will, can be processed in the multiplistic two-states-identified-as-one-so-no-single-exclusive state, as virtual and unobserved entities. In the multiplistic state they can be amplified, recorded, put onto tape, modulated onto RF signals, etc. And by our ordinary, objective, three- law science nothing is processed. And nothing indeed is what is there – a very special, structured, detailed, virtual set of nonexclusive, hidden-variable nonthings that is part of the new reality existing in the framework of the new four-law logic. In fact, this processable, structurable, nonobjective reality exists outside objective, three-law spacetime and is the basis for all psychotronic phenomena.
To our present monocular detection devices and monocular theory, such multiple-state entities are unobserved and hence are zeroes. They are pure vacuum, pure space, pure nothing, pure emptiness. But they are very real indeed, and they do physically exist, but multiocularly rather than monocularly.
The importance of the time interaction in explaining the two-slit experiment was noted as early as 1957 by Charles Musés in his introduction http://www.cheniere.org/references/muses/index.html to Jerome Rothstein’s Communication, Organization, and Science (Falcon’s Wing Press, Indian Hills, Colorado, 1958). Musés pointed out that the celebrated wave-particle paradox remains a paradox only so long as the chronotopological phases of the phenomena are left unrealized in the analysis. The entire foreword by Musés is a remarkable document that analyzes the structure of time itself.
Next Chapter http://www.cheniere.org/books/excalibur/photon quenching.htm
## Why Quantum Mechanics Is Not So Weird after All, from the ‘Comittee for Skeptical Inquiry’ from http://www.csicop.org/si/2006-04/quantum-mechanics.html
Richard Feynman’s “least-action” approach to quantum physics in effect shows that it is just classical physics constrained by a simple mechanism. When the complicated mathematics is left aside, valuable insights are gained.
by PAUL QUINCEY
The birth of quantum mechanics can be dated to 1925, when physicists such as Werner Heisenberg and Erwin Schrödinger invented mathematical procedures that accurately replicated many of the observed properties of atoms. The change from earlier types of physics was dramatic, and pre-quantum physics was soon called classical physics in a kind of nostalgia for the days when waves were waves, particles were particles, and everything knew its place in the world.
Since 1925, quantum mechanics has never looked back. It soon became clear that the new methods were not just good at accounting for the properties of atoms, they were absolutely central to explaining why atoms did not collapse, how solids can be rigid, and how different atoms combine together in what we call chemistry and biology. The rules of classical physics, far from being a reliable description of the everyday world that breaks down at the scale of the atom, turned out to be incapable of explaining anything much more complicated than how planets orbit the sun, unless they used either the results of quantum mechanics or a lot of ad hoc assumptions.
But this triumph of quantum mechanics came with an unexpected problem-when you stepped outside of the mathematics and tried to explain what was going on, it didn’t seem to make any sense. Elementary particles such as electrons behave like waves, apparently moving like ripples on a pond; they also seem to be instantaneously aware of distant objects and to be in different places at the same time. It seemed that any weird idea could gain respectability by finding similarities with some of the weird features of quantum mechanics. It has become almost obligatory to declare that quantum physics, in contrast to classical physics, cannot be understood, and that we should admire its ability to give the right answers without thinking about it too hard.
And yet, eighty years and unprecedented numbers of physicists later, naked quantum weirdness remains elusive. There are plenty of quantum phenomena, from the magnetism of iron and the superconductivity of lead to lasers and electronics, but none of them really qualifies as truly bizarre in the way we might expect. The greatest mystery of quantum mechanics is how its ideas have remained so weird while it explained more and more about the world around us.
Perhaps it is time to revisit the ideas with the benefit of hindsight, to see if either quantum mechanics is less weird than we usually think it is or the world around us is more so.
Classical Mechanics in Action:
When we think of planets orbiting the sun, we usually adopt Newton’s view that they are constantly accelerating-in this case changing direction-in response to gravitational forces. From this, we can calculate the motions precisely, and the impressive accuracy of predictions for total solar eclipses shows how well it works.
There is, however, another way of thinking about what is happening that gives exactly the same results. Instead of the Principle of Acceleration by Forces, as we might call it, there is an alternative called the Principle of Least Action, or more correctly, Hamilton’s Principle.
It is a principle that was first put forward about fifty years after Newton’s, in its earliest form by the Frenchman Pierre Maupertuis, and in its ultimate form by the Irishman William Rowan Hamilton.
The general idea is that when a planet travels through space, or a ball travels through the air, the path that is followed is the one that minimizes something called the action between the start and end points. Action, for our purposes here, is just something that can be measured out for some particular object moving along a particular path. It is exactly defined and is measured in units of energy multiplied by time. The details are not important unless you need to make calculations.
We therefore have two quite different ways of describing situations in classical physics that are equally good in terms of giving the right answer. To give the simplest possible example, we can think of a golf ball travelling across an idealized, frictionless, flat green. In Newton’s view (figure 1), the ball moves in a straight line at constant speed, because that is what Newton’s Law says it must do. In Maupertuis’ view (figure 2), the ball does this because this path is the one that has the least action between the start and end points. This trivial example can be made more interesting by making the green have humps and dips, which are like having forces acting on the ball, but the principles stay the same.
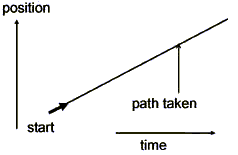
Figure 1. Classical mechanics-Newton’s view: the ball moves in a straight line at a constant speed, because that is what things do when there are no forces acting on them.
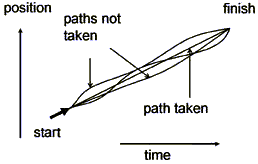
Figure 2. Classical mechanics-Maupertuis’ view: the ball moves in a straight line at a constant speed to any given point on its travels, because that is the path of least action between the start and finish.
Hamilton’s Principle is fundamentally equivalent to Newton’s Laws, and comes into its own when solving more advanced types of classical problems. But as an explanation, it has a major flaw-it seems to mean that things need to know where they are going before they work out how to get there.
Actually, this is where classical mechanics makes its first big step toward quantum mechanics, if only we look at it another way. The mathematics of Hamilton’s Principle can be described in words alternatively like this: given its starting points and motion, an object will end up at locations that are connected to its starting point by a path whose action is a minimum compared to neighboring paths. If locations away from the classical path are considered, no such paths exist-there will always be a path with the least action, but this is not a minimum.
It is an unfamiliar idea, but well worth a little effort to try and digest. One vital change to note is that, while still being classical physics, the emphasis has moved away from knowing the path that is followed to having a test to check whether possible destinations are on the right track. And the crucial factor is being able to compare the actions of different paths.
It leads to a third picture for our moving golf ball, central to the later move to quantum physics, which we can call Feynman’s view of classical physics (figure 3).
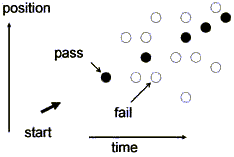
Figure 3: Classical mechanics-Feynman’s view: the ball is found at the black points, which happen to lie on a straight line, and not the white points, because only the black points pass the “action test.” This means that there is a path from the start to the black points whose action is a minimum compared to neighboring paths, but there is no such path from the start to the white spots.
If we stay within the world of classical physics, we can choose to ignore this strange new description and stick with the more comfortable idea that things are accelerated along paths by forces, but this would be a personal preference rather than a rational one. The new view prompts the question: “How do things work out whether possible destinations are linked to the start by a path of minimal action?” We should appreciate, however, that the old Newtonian view prompts equally difficult questions like: “How do things respond to forces by accelerating just the required amount, instant by instant?” Moreover, as we will see, the action version is the one that the world around us seems to use.
Roll on, Quantum Mechanics:
Suppose we take the action question seriously and give it a rather simple answer: Nature has to check out all possible destinations to see if they are on the right track. It must do this by trying to find out if there is a path of minimal action to each destination. It uses a device that can measure the action along all possible paths to each destination.
The device is a simple surveyor’s wheel for measuring action-just a wheel with a mark on the rim (figure 4). There isn’t literally a type of wheel that measures action, but we can imagine that there is. The mechanism assigns probabilities to each destination according to whether, with just this simple measuring tool, it can find a path of minimal action.
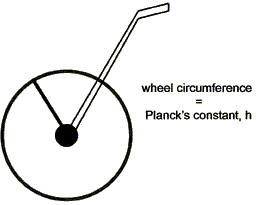
Figure 4: The single most potent image of quantum mechanics- a surveyor’s wheel for measuring action
When the actions it is trying to measure are large compared to the size of the wheel, the system typically works just as classical physics requires. But in some situations the mechanism fails to produce classical mechanics and gives us quantum mechanics instead. We call the circumference of the wheel “Planck’s constant,” after Max Planck, who discovered its importance by an indirect route in 1900.
You may be wondering how exactly the wheel can tell us what we need to know, but we don’t need to go into the details here-those interested should read Richard Feynman’s book, QED: The Strange Theory of Light and Matter, or see the summary given in the box on page 43.
Differences from Classical Physics:
As we might expect, the introduction of a mechanism for carrying out classical mechanics only makes a difference when the mechanism can’t do its job properly. Specifically, if we want to check out destinations that are too close to the start, as gauged by the size of the wheel, the mechanism doesn’t work. It cannot say where the object should be going, and there is an intrinsic fuzziness associated with it, with a scale set by the amount of action known as Planck’s constant. This is otherwise known as the Uncertainty Principle.
A second feature arises from the simple circular nature of the measuring device. It cannot tell the difference between paths that differ by an amount of action that is an exact whole number of Planck’s constants. This can lead to patterns of probabilities that look just like classical waves, because the mathematics of waves is very similar to the mathematics of circular motion.
The most important change comes when we consider objects in very small orbits, like electrons around nuclei. The mechanism gives zero probability unless the orbit (or more correctly the state) has an action that is an exact multiple of Planck’s constant. This crude mechanism explains why atoms can only shrink to a certain point, to a state with an action of Planck’s constant, where they become stable.
With one extra idea, which we will mention later, the mechanism seems to explain the workings of chemistry, biology, and all the other successes of quantum mechanics, without ever really stopping being classical mechanics.
Three Conceptual Problems with Quantum Mechanics:
The way it is normally introduced, quantum mechanics is something quite baffling, and certainly stranger than just classical mechanics with a mechanism. It is worth addressing the three most obvious difficulties directly:
1) Quantum mechanics gives answers that are a set of probabilities all existing at the same time. This is totally unreal. As Schrödinger pointed out, quantum mechanics seems to say that you could create a situation where a cat was both alive and dead at the same time, and we never see this. But this is in fact a very curious piece of ammunition to use against quantum mechanics.
We already have a very good nontechnical word for a mixture of possibilities coexisting at the same time-we call it the future. Unless we believe that all events are predetermined, which would be a very dismal view of the world, this is what the future must be like. Of course, we never experience it until it becomes the present, when only one of the possibilities takes place, but the actual future-as opposed to our prediction of one version of it-must be something much like what quantum mechanics describes. This is a great triumph for quantum mechanics over classical mechanics, which by describing all events as inevitable, effectively deprived us of a future.
Of course, there is now a new big question of how one of the possibilities in the future is selected to form what we see as the present and what becomes the past, but we should not see the lack of a ready answer as a fault of quantum mechanics. This is a question that is large enough, encompassing such ideas as fate and free will, to be set aside for another time. The headline “Physics Cannot Predict the Future in Detail” should be no great embarrassment.
2) Quantum mechanics means that there is a kind of instant awareness between everything. This is quite true, but by introducing quantum mechanics in the way that we have, the “awareness” is of a very limited kind-limited to the awareness gained through the action-measuring mechanism as it checks all possible destinations. It is very hard to see how the only result of this-a probability associated with each destination-could be used to send a signal faster than light or violate any other cherished principle. It is rather revealing that one of the few novel quantum phenomena is a means of cryptography-a way of concealing a signal rather than sending one.
3) Quantum mechanics doesn’t allow us to say where everything is, every instant of the time. This is the most interesting “fault” of quantum mechanics, and it can be expressed in many ways: particles need to be in more than one place at a time; their positions are not defined until they are “observed”; they behave like waves. We will summarize this as an inability to say exactly where particles are all the time.
The “classic” illustration of this is the experiment of passing a steady stream of electrons through two slits (figure 5). Instead of the simple shadows we would expect if the particles were just particles, we see an interference pattern, as if the electrons have dematerialized into a wave and passed through both slits at the same time.
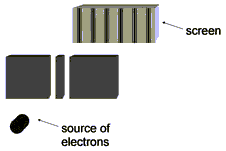
Figure 5: A schematic diagram of the two-slits experiment
There are several ways of coming to terms with this. The first thing to note is that the lack of complete information is not really a problem that arose in quantum mechanics-it originates in the third version of classical mechanics. In the Feynman version, the essence of motion is a process of determining if a destination is on or off the right track. Before the move to quantum mechanics, we can do this as often as we like, so that we can fill in the gaps as closely as we like, but the precedent has been set: physics is about testing discrete locations rather than calculating continuous trajectories. If it is inherent in old-fashioned classical physics, not just “weird” quantum physics, perhaps we can relax a little.
The second point is to clarify what the problem is. To take the two-slit example, we never see electrons dematerialize, or rippling through something, we just find it necessary to think that they do to explain the pattern that we see on the screen. If we deliberately try to observe where the electrons go, we see them as particles somewhere else, but the interference pattern disappears. In effect, the problem is that we cannot say what the particles look like only when they cannot be seen.
Now this is an uncomfortable thought, because all our instincts tell us that particles must be somewhere, even when we cannot see them. But if quantum mechanics can accurately describe all the information we can ever obtain about the outside world, perhaps we are simply being greedy to ask for anything more. The headline “Physics Fails to Describe Events That Cannot Be Observed” is, again, rather lacking in impact.
The final point is a little vague but more fundamental. If we accept that the future is not fixed, we expect it to contain surprises. Crudely speaking, this is not very plausible in a world where particles have continuous trajectories and an infinite amount of information is freely available. It is much more plausible in a world that is in some way discontinuous, where the available information is limited. Even though we have set aside the question of how a future full of possibilities turns into an unchanging past, it must involve something that seems pretty weird compared to our normal experience. Perhaps this example of physics not conforming to our expectations is weirdness of the right sort.
The Addition of Spin:
It was mentioned earlier that another new idea is needed before the classical physics of electrons and nuclei properly turns into chemistry. That idea is spin, a third property of electrons and nuclei alongside mass and electrical charge. Paul Dirac showed that spin is a natural property of charged particles within quantum mechanics. Wolfgang Pauli showed that the spin of the electron prevents more than one electron occupying the same state at the same time-the Exclusion Principle-a fact responsible for the whole of chemistry. The details are not important here, but quantum mechanics with spin seems to account for pretty much all the world we see around us.
Quantum Mechanics-Bringer of Stability:
One of the benefits of viewing the quantum world as not fundamentally different from the classical world is that we can imagine how one changes into the other. With a few simple assumptions, a classical world of point-like electrons and nuclei is blindingly chaotic. Atoms are continually trying to collapse, but are prevented from doing so by the huge amount of electromagnetic radiation that is released in the process. It is not the comfortable place that the word classical implies.
As we imagine moving to the quantum realm by increasing the size of Planck’s constant from zero, something remarkable happens. At some point, the blinding light disappears to reveal stable atoms, capable of forming molecules. Far from making everything go weird, quantum mechanics makes it go normal. To be sure, if Planck’s constant increases too far, the atoms fall apart and a different form of chaos takes over, but that just makes the story even more interesting.
So it seems that quantum physics is not weird and incomprehensible because it describes something completely different from everyday reality. It is weird and incomprehensible precisely because it describes the world we see around us-past, present, and future.
Reference:
Feynman, Richard P. 1985. QED: The Strange Theory of Light and Matter. Princeton, N.J.: Princeton University Press.