Final Secret of Free Energy Additional, by Tom Bearden,
extracts from http://www.cheniere.org/techpapers/Final%20Secret%20of%2015%20Feb%201994/index.html
Additional Information On The Final Secret of Free Energy, Update 15 February 1994, © 1994 by T.E. Bearden
Introduction
My associates and I have filed the first patent application on two electrical overunity processes and devices; one similar to what is outlined in The Final Secret of Free Energy [Ref 1] and an additional variation utilizing, as collectors, standard step-charged capacitors rather than degenerate semiconductor materials. In 60 to 90 days, we will have a very enlightening paper (more likely a book) ready on that. We also plan to file several more extremely fundamental overunity patent applications from additional phenomena and mechanisms that we have uncovered.
In this paper, it is assumed that the reader is familiar with the content of The Final Secret of Free Energy. Figure 1 shows the invention schematically, and we briefly summarize it as follows:
Summary of the Invention
A method and apparatus for extracting bidirectional EM wave energy from the vacuum through the scalar potential gradient across the terminals of an electrical source, collecting the excess energy in a collector without entropy, then separately discharging the collected energy through a load to perform work, without sending the load current back through the primary source against its potential gradient; i.e., against its back emf.
Removing the load current from the source thereby substantially reduces the production of work inside the source to dissipate its bipolarity; said internal dissipative work being well-known to be the cause of exhaustion of the source’s ability to continue to furnish emf to the external circuit. By reduction of its internal dissipation, the source is enabled to furnish more energy for dissipation in the external load than is utilized to dissipate the source internally. Hence the source is enabled to operate with an overunity operational efficiency.
The system permissibly operates as an “open” system, and extracts and utilizes excess EM energy from a free-flowing external source (the flux exchange between the surrounding vacuum and the bipolarity of the source), hence it can operate at an efficiency greater than unity without violation of the laws of physics, in a manner analogous to but entirely different from a heat pump. In this invention, it is not the purpose of the primary source to furnish current and dissipative power to the external circuit. The bipolarity of the source is utilized primarily as a dipole antenna to receive the bidirectional EM wave energy flow from the vacuum, and direct it without entropy through a switching unit to the collector. Conduction electrons in the collector are temporarily restrained while being overpotentialized by the excess energy being collected upon them. The collector and its overpotentialized electrons are then switched away from the primary source, and connected across the load as a separate circuit and closed current loop. The electrons in the collector and their excess energy are then automatically released to flow as current discharge through the load, releasing their excess energy to perform useful work in the load. The collector is then switched away from the load and back across the primary source, and another collection cycle is initiated. Iteration of the collection and discharge cycles provides power to the load. Additional collection and smoothing capacitances for smoothing the iterations and furnishing steady power to the load may be added as desired. The invention violates the closed circuit practice of powering loads, but does not violate the conservation of energy law, the second law of thermodynamics, or any of the other known laws of physics.
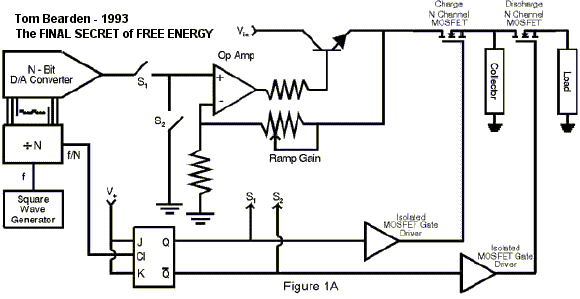
Figure 1a. Type circuit utilized for ramp-up charging of a capacitor without work, and separate discharge of the collected energy in the load without substantial depletion of the primary source.
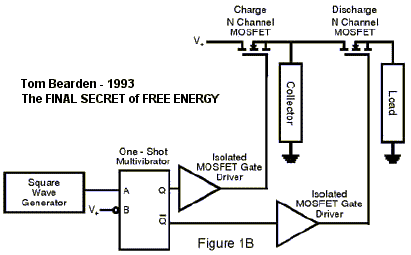
Figure 1b. Type circuit for single pulse charging of a degenerative semiconductor collector without appreciable work, and separate discharge of the collected energy in the load without substantial depletion of the primary source.
Use of Step-Charged Capacitor as the Collector
Fulfilling our search for a special material with the extended electron gas relaxation time for the collector, a material alloy composed of 98% aluminum and 2% iron is tentatively suggested. However, production of this alloy is particularly difficult, so we are still researching for a solution that is more easily manufactured.
Meanwhile, the necessity for using a special material for the collector has been bypassed by another procedure we have utilized. Rigorously one can use a normal capacitor as the collector, if one step-charges it in several hundred small incremental rectangular voltage steps (stair-step-charging). The proof that this can freely charge a capacitor with energy, without having to do appreciable work, is already known in the literature. You can charge the capacitor without entropy and essentially without drawing electron mass current. [Ref 2,Ref 3,Ref 4,Ref 5]
Actually we consider the capacitor to be charged by massless displacement current flow, which for circuitry purposes we consider to be d#/dl — a flow of pure potential (trapped EM energy) along a conductor or through the vacuum; i.e., under conditions where mass displacement current flow does not exist. [Ref 6, Ref 7]
Massless Displacement Current Is Freely Available From Any Source
The principle embodied in the invention is that one can extract all the free EM energy one wishes, from any electrical power source, as long as it is extracted via massless displacement current and not by electron mass flow current. [Ref 8] And one can freely collect this extracted energy from a source into an ordinary capacitor if one does it correctly, because one can charge the capacitor via massless displacement current without expending any appreciable work inside the source to dissipate its dipolar separation of charges.
Every Electrical Source of Potential Is Already a Free Energy Source
We thus advance a revolutionary concept: all present power systems already utilize free energy source-antennas. However, the standard two-wire closed circuitry diabolically utilizes one-half the total free energy extracted by the source-antenna from the vacuum, to perform work inside the source-antenna to dissipate its dipolarity and hence to dissipate the source-antenna (i.e. the receiver) itself.
The source already acts as a “dipolar antenna” to continually receive “scalar potential” current d/dl (massless displacement current) from the vacuum. [Ref 9] Previously scientists and engineers have simply ignored this special massless EM energy influx. For load-free (i.e., mass-current-free) conditions, (d/dl) is continually received from the vacuum by any dipole (i.e., by any dipolar source-as-an-antenna), and the flowing energy is continually exchanged back and forth between the vacuum and the dipole.
This free energy exchange with the vacuum is also true of any two points in our circuit that possess an open-circuit voltage or potential difference between them. Two such points act as a dipole. Free energy dipolar antenna sources are everywhere; we just have to learn how to break the symmetry in their energy flux exchange with the vacuum, collect some of the freely flowing influx, and distribute that collected excess energy to an isolated load to separately power it.
In other words, we simply have to implement circuitry that operates analogous to the standard heat pump cycle.
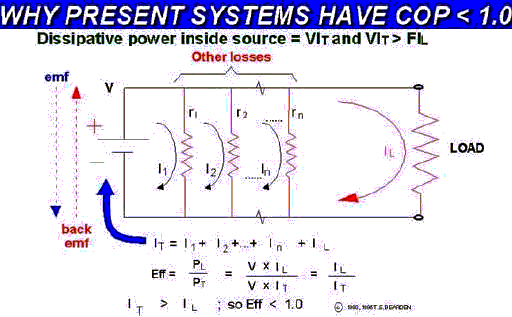
Figure 2. Why present electrical power systems have underunity operational efficiency.
Conventional 2-Wire Closed Circuit Operation
In the conventional 2-wire system a load is added to the source-antenna, allowing circulation of electron current in a closed circuit through the load and then through the ground return line back to and through the dipolar source-antenna. The only useful reasons for this “closed circulation” of the electrons are (1) it is simple, easy, habitual, and accepted, (2) all our components, instruments, and methodologies are developed in accordance with this usage, (3) one uses the electrons as a working material fluid to receive, transport, and discharge excess EM energy, and (4) forcing the electrons back through the back emf reloads the spent electrons again with excess EM energy in the form of little $#’s (excess trapped energy density) upon each recycled electron.
Some of the excess $# collected upon the electrons is expended in the load as useful work, but one half of the total is expended in driving the spent (without excess $# Consequently all conventional 2-wire circuits, which return all external electron-flow current loops back through the source, are always underunity devices, as is shown in Figure 2. Eerily these conventional sources are already free energy devices, which are unwittingly attached to circuitry specifically designed to utilize part of their freely received energy to deplete or destroy themselves, i.e., they are already open systems receiving free energy from the vacuum, but they are hooked up and designed in a suicidal manner so as to use at least half of that freely extracted energy to re-close the system and shut off the influx of free energy. Since at least some of the remaining half of the energy is lost in inefficiencies, frictional losses, etc., less than half the total free energy goes to the load. So there is always less useful work being done in the load than the destructive work being done inside the free-energy source-antenna to destroy it.
Operational Efficiency
We define operational efficiency Alpha as the average power expended in the load to power it, divided by the average power expended inside the source to dissipate its dipolarity. If Alpha 1, then if the additional losses are minimal, the device can conceivably run itself while furnishing some energy to a load to produce useful work.
We Must Excise the Suicidal Closed Circuit To Achieve Overunity
There is no mysticism in the overunity electrical device. The device is an open system that extracts excess energy from the vacuum, collects it, and transports it to the load to separately power the load. It is simply analogous to the standard heat pump cycle. It is also directly analogous to presently operating overunity systems such as windmills, waterwheels, solar cell arrays, and hydraulic turbines in a dam installation. All that we have done is to eliminate or dramatically reduce the standard cancerous mistake in conventional electrical power systems wherein much of the excess energy freely extracted from the vacuum by the already-overunity electrical source is then utilized to destroy the source’s energy reception ability!
As we stated, in the conventional electrical device and circuitry, more destructive work is always done inside the source than is done usefully in the external load. Hence the conventional operational efficiency is always underunity.
Legitimate Overunity Systems Comply With Well-Known Requirements
There are many alternative and well-known permissible free energy systems that operate at overunity operational efficiency: solar cells, windmills, hydraulic turbines, heat pumps, and water wheels, to name a few. All of these are open systems, receiving an influx of free energy from a natural energy flow, and collecting and gating some of that energy to be dissipated in a load to do useful work. All of them are permissible overunity devices, since (1) they are open systems, (2) they constantly receive a free energy influx from an external source, (3) they extract and collect some of this energy without dissipation, (4) they dissipate this collected energy in a load, and (5) the discharge process is totally separated and isolated from the “collection-from-the-source” process.
No Legitimate Overunity System Is Intentionally Made Self-Destructive
Not a single one of these open overunity systems foolishly uses part of its freely extracted and collected energy to re-close the system and shut off its influx of free energy flow! What engineer would build a solar array such that, the moment the current started to flow, it powered a shutter arrangement to gradually close and shield off the solar array from the sun? Who would build a windmill so that, whenever the angled-blade assembly rotated in the wind to furnish power, a gearing feedback assembly also slowly caused the individual blades to rotate into a position parallel to the wind, thus stopping the windmill?
Yet this is precisely what the conventional electrical power system does with its external circuit. It deliberately utilizes half of the freely extracted energy to re-close the system and shut off the free energy flow between the vacuum and the source-antenna, by destroying the receiver-antenna!
However, this “suicide circuit” practice is guaranteed to keep the power meter on your home or business, and to keep the meter on the gas pump for fueling your automobile. Perhaps one may be forgiven for suspecting that, at the deepest levels of financial control, this may be the real purpose in seeing that the existing interpretation of classical EM stays “as is.”
All Electrical Power Sources Are Already Free Energy Receiving Antennas
All conventional electrical power systems already contain fully functional free energy systems in their source component. Each conventionally designed system is, however, deliberately suicidal, since part of the system’s own energy is utilized to work against itself and destroy itself. This is primarily due to the preoccupation of engineers with power and work. They do not consider the source as an energy source, but as a power source. Power being the time-rate of performing work, and work being the dissipation of energy, they are thus naturally conditioned to think of the “dissipation of the source” as its natural functioning.
In fact, hardly a single one of them is aware that EM energy itself is a free-flowing process. Only a finite collector possesses a finite collection of EM energy. In nature, the potential gradients of all dipoles are already rivers of free-flowing EM energy exchange with those dipoles, where the energy density is freely furnished and is essentially free for the taking. It is mind-boggling that we have all been conditioned to extract this free energy furnished by nature and the creator, but to always utilize half of the extracted energy to destroy the receiver-antenna and thus strangle the flow!
In our work, we simply have excised this “self-destructive” cancer and reworked the circuitry so that only a minimal amount of the freely extracted energy is utilized for internal destruction of the source-antenna.
Thermodynamics and Open Overunity Systems Not In Equilibrium
In our approach we have an open system during every collection cycle, with an external source of energy and a continual energy influx. We have deliberately broken the local symmetry of the system’s energy exchange with the vacuum, by spatially and temporally separating the energy collection and energy discharge phases. Overunity operational efficiency is permissible for such a system without violation of any of the laws of nature. Some of the influx of excess energy from the vacuum into the dipolar source antenna is transported without loss to the collector and collected. The collected energy in the collector is then separately discharged through the load, without any of it being discharged back inside the source-antenna. Note that we have broken local energy flow equilibrium but not global energy flow equilibrium.
The second law of thermodynamics, e.g., does not even apply to such an open system not in equilibrium. Classical thermodynamics cannot even compute the entropy of an open system not in thermodynamic equilibrium, as is well-known to thermodynamicists. [Ref 10]
What classical thermodynamics does have to say, is that such an open system must contain excess energy when compared to the closed system in equilibrium, because the closed system in equilibrium is in the maximum entropy condition. [Ref 11] Global conservation of energy is not violated, just as it is not violated in a windmill or in a heat pump, which are similar open systems. Local conservation of energy (which applies only to a closed system or to a system in total equilibrium) does not apply because the system is open and not in equilibrium.
Permissible Electrical Overunity Is Not Perpetual Motion
An open system out of equilibrium need not conform to (1) the local (closed system, equilibrium conditions) conservation of energy nor to (2) the second law of thermodynamics (which assumes equilibrium conditions). It must and does conform to the global conservation of energy, just as does a waterwheel or windmill. We strongly stress that the overunity electrical device is not a “perpetuum mobile.” [Ref 12] The electrical operations and systems we propose are perfectly permissible by the known laws of physics and do not violate any of them. We propose a permissible series of overunity electrical systems.
The Heat Pump Analogy
In one way of viewing it, all we have done is utilize the potential as a more modern type of quantum mechanical fluid having hidden bidirectional flowing EM energy. [Ref 13], Ref 14, Ref 15, Ref 16] QM already certifies that the potentials, not the force fields, are the primary causes of all EM phenomena. Contrary to classical EM theory, the force fields are effects in, on, and of the charged particles themselves. Consequently, if the potentials are the primary causes of all EM phenomena, then for free energy to perform work (free causes to collect and generate desired effects) we must turn to the potentials.
We have utilized a hookup and switching arrangement so that energy-free collection is totally separated from collected energy discharge in the load. In short, we have done what a normal heat pump does, when it uses the air with its thermal energy as a working energy-containing fluid. Consequently, overunity operational efficiency of analogous electrical devices is perfectly permissible, and not prohibited by the known laws of physics.
An Electrical Power Source Is a Dipolar Antenna For Free Reception of Energy
An electrical power source is in fact only a dipolar antenna for reception of potential (hidden bidirectional Whittaker/Ziolkowski waves). All the current you run back through the back emf of the source, to perform dissipative work inside it, is something you yourself are doing to the source. It is not a priori a characteristic of the source!
If no work is done inside the source’s internal bipolar separation of charges (i.e., if no electron or ion current is forced back up from the ground return line against the source-antenna’s potential and therefore against its back emf), then the dipolar source-antenna will last essentially forever, or until something corrodes or breaks mechanically.
The flow exchange of energy between the vacuum and the dipolar source-antenna is freely driven by all the charges of the universe, in accordance with Puthoff’s cosmological feedback loop. [Ref 17]
Massless Displacement Current
Technically one is using massless displacement current to charge the capacitor, rather than electron mass flow current. It is real energy flow nonetheless; just in work-free, dissipation-free form. As is well-known, one plate of a capacitor already charges the other plate by just this very massless displacement current, transporting real EM energy across the gap between the plates in the process. The electrons themselves do not cross the gap.
Displacement current is already well-known to be “free” energy transport without any dissipation as power and work. By drawing massless displacement current only from the source-antenna instead of electron flow current, you can draw work-free, dissipation-free energy as long as you wish, as often as you wish, and as much as you wish, without ever dissipating the source-antenna. You just have to collect it onto some trapped electrons or other charges, such as in a capacitor’s plates, then switch the collected energy (charged capacitor) separately across a load, in a separate discharge circuit, to discharge through the load as work.
The real trick is to prevent the electrons in the circuit from moving and providing mass “energy dissipation” current inside the source during the collection process. In the original paper, we explained that this could be done by using as a collector a degenerate semiconductor material, with extended electron gas relaxation time. In this paper we have explained how this can be done by step-charging an ordinary capacitor as a collector. We have also included specific references proving (both experimentally and theoretically) that this is correct. With the requirement for special materials removed, there is no reason that a competent researcher cannot develop a step-charged capacitor device to prove it experimentally for himself or herself.
Requirement: Proof of Principle and Independent Test and Certification
My associates and I are proceeding as rapidly as possible toward full-up “proof-of-principle” circuits for open release and certification or falsification by the scientific community and engineers at large. Soon we also expect to release to other researchers information on the kinds of new electrical phenomenology one meets in true overunity electrical devices. These are not in the textbook, at least with respect to electrical power systems. We give some indication of these phenomena below:
New Circuit Phenomena Must Be Mastered
One meets unusual electrical phenomena in attempting to perform overunity electrical operations. For overunity, a priori one must “slip excess potential” through the circuit essentially without losses. That is, one must deliberately pass massless displacement currents through the circuit and at least through some of its components.
Solid-state switching components in particular exhibit unusual phenomena, to say the least, when excess potential is introduced into and through all their internal components inside modern semiconductors. An ordinary MOSFET, e.g., may have 25,000 separate internal components. It is as if someone crammed the entire electronic parts store inside it. Simple switches these semiconductors are not, when exposed to appreciable massless displacement current.
When one “slips in” some pure potential, by SWZ decomposition one has also slipped in some bidirectional EM pump waves. The nonlinear semiconductor materials will function as phase conjugate mirrors when suitably pumped, including at non-optical frequencies. Consequently pumped phase conjugate replicas, self-targeting, formation of quantum potentials, and modular variable effects sometimes begin to evidence. We will address and explain some of these effects in a future paper. For now, we simply state that they occur, and there is a host of extra phenomenology the experimenter may encounter.
However, an iron rule for the experimenter is that, for odd circuit behavior, first exhaust all “normal” causes before turning to the extraordinary causes. One will save oneself a great deal of grief by applying this Occam’s razor.
Also in deliberately utilizing displacement current, one is actually employing an expanded, higher topology EM with additional degrees of freedom, similar to that pointed out by Barrett. [Ref 18] Consequently one encounters a host of additional higher topology EM phenomenology. In particular one encounters nonlinear optical (NLO) functioning of the semiconductors at any and all frequencies, not just in optical bands.
Overunity Electrical Devices Are Permissible By The Laws of Physics
The overunity electrical energy system is permissible by the laws of physics and is not in any manner perpetual motion. It simply extracts excess EM energy from an ubiquitous source, through a dipole as a receiver, and collects that excess energy, conducts it to the load, and separately dissipates it in the load to power the load, without using any of the collected energy to perform work inside the source to dissipate the source-antenna. It is directly analogous to a heat pump, which is well-known to perform at overunity operational efficiency under nominal conditions.
In Conclusion
Primarily my associates and I believe we have corrected an ubiquitous error made in present power systems that prevents these systems from realizing their already-inherent overunity operational efficiency. We also firmly believe that the permissible electrical overunity device is an idea whose time has finally come.
Notes and References
1 – T. E. Bearden, “The Final Secret of Free Energy,” distributed over the Internet, Feb. 9, 1993. The paper was also published in Magnets, 7(5), pp. 4-26 (1993); in Explore!, 4(3/4), pp. 112-126 (1993), and in several other media.
2 – For proof that you can charge an ordinary capacitor almost without entropy, see I. Fundaun, C. Reese, and H. H. Soonpaa, “Charging a Capacitor,” American Journal of Physics, 60(11), pp. 1047-1048 (1992). A capacitor can be step-charged in small steps to dramatically reduce the entropy required to charge it. In the limit, a theoretically perfect capacitor can be fully charged without any electrical current or work at all, i.e., you can simply transport the excess energy density (the potential gradient) of the open circuit voltage of the source to the collector, and couple thatto the electrons trapped in the capacitor plates, without electric current from or through the source.
3 – M. G. Calkin and D. Kiang, “Entropy Change and Reversibility,” American Journal of Physics, 51(1), pp. 78-79 (1983).
4 – F. Heinrich, “Entropy Change When Charging a Capacitor: A Demonstration Experiment,” American Journal of Physics,54(8), pp. 742-744 (1986).
5 – V. K. Gupta, Gauri Shanker, and N.K. Sharma, “Reversibility and Step Processes: An Experiment for the Undergraduate Laboratory,” American Journal of Physics, 52(10), pp. 945-947 (1984).
6 – In most texts the treatment of displacement current is far from adequate. A better treatment than most is given by John D. Krauss, Electromagnetics, Fourth Edition, McGraw-Hill, New York, pp. 437-439, 547-549 (1992). Additional useful insight can be gained from David J. Griffiths, Introduction To Electrodynamics, Second Edition, Prentice-Hall, Englewood Cliffs, New Jersey, pp. 304-308 (1989). Problem 7.51 on p. 335 is also of direct interest, as is particularly the comment by Griffiths below the problem. Additional insight can be gained from David Halliday and Robert Resnick, with assistance by John Merrill, Fundamentals of Physics, Extended Third Edition (1988), John Wiley & Sons, New York, vol. 2, Article 37-4: Displacement Current, pp. 836-837, 839-841. The standard notion is to (1) retain the continuity of current, thus modifying and salvaging Ampere’s law, (2) the displacement current is non-physical, i.e., it does not involve the transfer of charged mass, (3) focus primarily upon magnetostatics as to the results achievable by the displacement current, (4) retain the notion ofas E, a force field, thereby focusing the notion of displacement current upon the change of the E field without the flow of charged mass, and (5) retain the confusion between electrical charge and charged mass that is inherent in the terms “charge”, “current”, etc. On p. 836 Halliday and Resnick point out that the displacement current is not derived per se, but is a “fit” based upon symmetry arguments, and it must stand or fall simply on whether or not its predictions agree with experiment. On the same page the displacement current is taken to be a linear function of d/dt. For flow along a circuit where there is no electron mass current, it seems appropriate to replace d/dt by d/dl. It is also strongly indicated that one should clearly distinguish between charged mass current flow and the flow of massless charge, which is the approach we have taken.
A final indication of the way conventional scientists tend to regard displacement current is given by Martin A. Plonus, Applied Electromagnetics, McGraw-Hill, New York, pp. 446-448 (1978). Here Plonus uses the prevailing notion of the E field being altered by the flow of massless displacement current. As can be seen, the displacement current is relegated almost to a curiosity of capacitors, and not really too essential except just to “balance the books” and retain Ampere’s current continuity.
We now wish to point out something very subtle but very rigorous. CEM erroneously uses E = – to equate a mass-free potential gradient with a mass-containing force field. This “E-field” only exists at a point when there is a point-coulomb of electrical charged mass at the point. The real version of this equation should be E == -[()q]/|q|, whereis the potential gradient coupled directly to the charged point-mass at the point, q is the number of coulombs of charged mass at the point, q/|q| is one coulomb of charged mass, and E now is properly the force on and of each coulomb of the collected charged mass at the point.
Viewed in this manner, one can now see that the E field may be altered by flow of additional charged mass q, or by flow of massless additional , or both. This is now in agreement with the manner in which it is approached in CEM, but more rigorous. Essentially it states we may increase the total “charge” (potential) at a point by either (1) moving in additional charged masses by use of a conventional current, or (2) moving in additional massless charge (potential) without any additional change in mass, or (3) a combination of the above.
However, let us apply this to a single charged particle or to a fixed number of them. No one seems to have noticed that the notion of altering the E-field of the collected point- charges at a point via method #2 , i.e. by a flow of massless displacement current onto the fundamental charged particles themselves, a priori requires the electrical charge of each fundamental particle to change. Hence it falsifies the notion of quantization of charge.
Also, no one seems to have noticed the electric power implications: if it is known that one can charge a capacitor purely by displacement current, then one can charge up the capacitor with energy, without any dissipation of the source, because only charged mass current through the back emf of the source does that. So one can then disconnect the charged capacitor and separately connect it in a closed circuit with a load, to discharge through the load and furnish free work in the load (free in the sense than no dissipation of the primary source occurred in either the collection of the energy or in discharge of the collected energy through the load as useful work). Free energy, overunity electrical devices, etc. should then be readily apparent and permissible, from the known nature of displacement current and capacitors alone.
7 – Maxwell assumed a material ether, which was assumed to be a thin material fluid filling all space. Hence force (which must have mass as a component due to its definition F == d(mv)/dt) could be modeled as existing in the Maxwellian ether, for there was already thin matter present everywhere. Hence in Maxwell’s EM the incorrect notion resulted that force fields existed in the vacuum. Oliver Heaviside continued this erroneous assumption, since in fact he hated the potentials, regarded them as mystical, and stated that they should be “…murdered from the theory.” Also, electricity was thought to be a similar thin material fluid. So the material electric fluid could and did flow through the fluid vacuum also, giving the notion of the material electric flux density for D. Consequently, the units of D are coulombs (charged mass rate of flow) per square meter. Rigorously, that material D flux exists only on and of charged mass that moves; it cannot and does not exist in vacuum. Only potentials and potential gradients exist in vacuum. However, after Maxwell’s formation of his theory, the Michelson-Morley experiment destroyed the material ether (not the ether per se, but its material nature). So electricians then simply proclaimed that they were no longer using the material ether, and that such did not exist! Not a single Maxwell/Heaviside equation was changed. The material ether is still very much assumed in classical EM (CEM) theory, and so the theory is accordingly very seriously flawed. Since CEM also has no adequate definition for either electric charge or the scalar potential, the problem is confounded.
To clarify this problem, one must separate the notion of electric charge from the notion of mass. The electrical charge of a charged mass is the virtual photon flux exchange between the surrounding vacuum and that mass. Since a virtual photon flux is just a scalar potential, the electron’s massless electrical charge is simply its scalar potential. It can now be seen that, if we forcibly remove the notion of “mass” from D in the vacuum, or in a charged material medium where the charged masses cannot move, then the “material electric flux concept” portion of D turns into d#/dt, a change in the nonmaterial electric flux. However, D is a vector and hence has a “net flux” spatial directional aspect which d#/dt alone does not possess. It follows that the value of d#/dt at a spatial point actually represents the result of change of the value of # at that point, as a function of time. Thus a directional operator must first be invoked upon # at the point, to provide a direction for the spatial #- current after the d/dt operator is invoked. The appropriate operator to give directionality to # is $, so that D in vacuum or in an electron-current-free charged medium becomes a function of d/dt(-$#). Conventionally, the use in the literature of E = -$# immediately provides that d/dt(-$#) at a point results in dE/dt, or the time rate of change of the E-field at that point. If no distinction is made between charged mass current flow and massless charge current flow, this would be true in either vacuum or material media. However, we wish to specifically distinguish between massive displacement current and massless displacement current. So we point out that the increase dE/dt in the magnitude of the E-field at, on, and of a charged particle at a point, can be due to either (1) the flow of mass current to build up the number of point coulombs at that given point, where each coulomb has a fixed massless charge (potential), or (2) the flow of massless current d/dt (-$#) so as to alter the value of # at that point, evidenced by a fixed number of coulombs of charged particles, each of which has altered its individual potential and therefore its individual massless electrical charge.
So what “flows” when the charged masses are frozen or absent is simply a current of scalar potential, resulting in a change of the potential upon fixed point charges of d#/dt. This is what crosses between the plates of a capacitor, e.g., which is where the notion of “displacement current” originated in the first place. (See, e.g., Halliday and Resnick, 1988, ibid., p. 836, Sample Problem 1, for expression of the displacement current as d#/dt, neglecting constants of proportionality). This is also what flows when one connects multiple open circuit pairs of conductors to a source.
It remains to examine Maxwell’s equation $.D = pv. If mass displacement current cannot flow, then there exists no divergence of the mass current portion of D. However, massless displacement current can still flow, and there can exist divergence of that component. There are now three aspects to that equation: (1) the case in the vacuum, where there exists no physical ? and hence no pv as such because of the absence of mass, (2) the case in a material medium, which is the normal case already treated in the standard equation and need not be further addressed, and (3) the case in a material medium where, nonetheless, physical charged masses such as electrons cannot move, but massless charge currents may still move. Only cases 1 and 3 need to be addressed, and they have the same treatment.
We address the one dimensional case, which is sufficient for circuit current flow considerations. First we replace D with (D# + Dp), where the first term is the massless displacement current and the second term is the massive displacement current. In other words, we account separately for charged mass flow and for massless charge flow. Similarly, we express pv as two components, one massive and one massless, so that pv = d/dl( # + mv). For case 1 and case 3 we make mv = 0 and Dp = 0. For those cases, we have $.D = $.D# = d#/dl (since current along a wire is a one-dimensional flow). We specifically note that #, D#, $.D, and d#/dl are not necessarily conserved quantities, sinceis mathematically decomposed into bidirectional EM waves, and is hence a freely flowing process. When symmetry is broken so that equilibrium conditions no longer exist, one or more of these quantities will not be locally conserved.
What has actually been done here is to open the classical EM model to the free exchange of massless EM energy that is always ongoing between any charged particle’s mass and the vacuum. We then account separately for the flow of the energy exchange (of the massless charge flow) and the flow of the physical receiver/transmitters (i.e., for charged mass flow). Our switching arrangement to separate the collection and discharge cycles constitutes a permissible “Maxwell’s Demon” which breaks symmetry, hence breaks equilibrium and opens the system as required. Since such a system can continually receive a free influx of energy from its external source, such a system can permissibly exhibit overunity operational efficiency without violating the laws of physics.
8 – Displacement current is already known to be lossless transport of energy without entropy, i.e., without work. For a typical confirmation see Jed Z. Buchwald, From Maxwell to Microphysics, University of Chicago Press, Chicago and London, p. 44 (1985). Quoting: “…no energy transformation into heat occurs for displacement currents.”
9 – We strongly stress again that the scalar potential may be mathematically decomposed into a harmonic series of hidden bidirectional EM wave pairs. Each wave pair consists of an ordinary EM wave together with its superposed phase conjugate replica wave. Thus internally the scalar potential gradient across a source represents a bidirectional exchange of EM wave energy with the surrounding vacuum. See notes 13, 14, 15, and 16 below for references confirming the decomposition of the “fixed” potential into a dynamic flow process and energy exchange process.
10 – For confirmation see Robert Bruce Lindsay and Henry Margenau, Foundations of Physics, Dover Publications, New York, pp. 283-287 (1963). See particularly p. 283, which emphasizes that a “field of force” at any point is actually defined only for the case when a unit mass is present at that point. See p. 17 on the limitations of a “natural law”; p. 213 and 215 for limitation of thermodynamic analysis to equilibrium states; and see p. 216 for definition of entropy. See p. 217 for the fact that the entropy for non-equilibrium conditions cannot be computed, and the entropy of a system not in equilibrium must be less than the entropy of the system in equilibrium, i.e., for a system to depart from equilibrium conditions, its entropy must decrease. Therefore its energy must increase. Thus the energy of an open system not in equilibrium must always be greater than the energy of the same system when it is closed and in equilibrium, since the equilibrium state is the state of maximum entropy.
11 – Lindsay and Margenau, ibid., p. 217.
12 – The basic notion in the perpetual motion conundrum is that somehow a closed system in thermodynamic equilibrium could perpetually provide external energy to a load outside the system. Such a notion is an oxymoron; if the system is closed, no energy can escape or enter, hence the system could not furnish energy externally to power a load or even just to radiate away. My associates and I have not in any manner proposed such a system or entertained the notion that such might exist. But it is well-known that open systems not in thermodynamic equilibrium can freely extract energy from their environment and furnish energy to power a load, and that is precisely what we have proposed.
13 – G. J. Stoney, “XLVIII. On a Supposed Proof of a Theorem in Wave-motion, To the Editors of the Philosophical Magazine,” Philosophical Magazine, 5(43), pp. 368-373 (1897).
14 – E. T. Whittaker, “On the Partial Differential Equations of Mathematical Physics,” Mathematische Annalen, vol. 57, pp. 333-355 (1903). Whittaker mathematically decomposes the scalar potential into a bidirectional series of EM wave pairs in a harmonic sequence. Each wave pair consists of the wave and its phase conjugate. (We have pointed out elsewhere that such a wave pair is a standing electrogravitational wave and a standing wave in the curvature of local space-time). To see that all classical EM can be replaced by interference of two such scalar potentials (i.e., by the interference of their hidden multi-wave sets), see E. T. Whittaker, “On an Expression of the Electromagnetic Field Due to Electrons by Means of Two Scalar Potential Functions,” Proceedings of the London Mathematical Society, Series 2, vol. 1, pp. 367-372 (1904).
15 – Richard W. Ziolkowski, “Localized Transmission of Electromagnetic Energy,” Physical Review A, 39, p. 2005 (1989). For related material, see Richard W. Ziolkowski, “Exact Solutions of the Wave Equation With Complex Source Locations,” Journal of Mathematical Physics, 26, pp. 861-863 (1985). See also Michael K. Tippett and Richard Ziolkowski, “A Bidirectional Wave Transformation of the Cold Plasma Equations,” Journal of Mathematical Physics, 32(2), pp. 488-492 (1991).
16 – C. W. Hsue, “A DC Voltage is Equivalent to Two Traveling Waves on a Lossless, Nonuniform Transmission Line,” IEEE Microwave and Guided Wave Letters, 3, pp. 82-84 (1993).
17 – H. E. Puthoff, “Source of Vacuum Electromagnetic Zero-point Energy,” Physical Review A, 40(9), pp. 4857-4862 (1989). Presents Puthoff’s self-regenerating cosmological feedback cycle for the source of the vacuum EM zero-point energy.
Our comment: Over any macroscopic range, the vacuum fluctuations (‘s) of the ZPE sum to a vector zero translational resultant. The individual ZPE components (‘s), however, are still present and active, and their energies are present as well. That vector zero can thus be considered to be a gradient-free potential, or the vacuum potential, since it contains enormously dense, trapped EM energy. So the vacuum potential — pure space-time (ST) itself — contains enormously dense EM energy.
One can then apply the Stoney/Whittaker/Ziolkowski (SWZ) methodology to decompose this powerful vacuum potential, i.e., the vacuum, and in fact space-time (ST) itself, into an incredibly dense flux of EM energy. Space-time is revealed to be an incredibly powerful electrostatic scalar potential. The electrical charge (potential) of a charged particle is a small potential gradient in the ST potential, i.e., it is a slight alteration of the local ST potential. Via Puthoff’s self-regenerative feedback cycle, the energy flowing in this potential is being exchanged between the local source and all the charges everywhere in the universe. This “potential gradient” or electrical charge itself can be decomposed via the SWZ approach, and becomes a bidirectional EM wave pair exchange of excess EM energy between the vacuum/ST and the charged particle’s mass. The potential gradient between the ends of a dipole have similar decompositions, with the additional characteristic that the negatively charged end of the dipole receives the forward-time waves from the SWZ wave pairs, and the positively charged end receives the time-reversed waves.
Our final comment is that Cole and Puthoff have rigorously shown that, in theory, the vacuum EM energy can indeed be extracted. See Daniel C. Cole, and Harold E. Puthoff, “Extracting Energy and Heat from the Vacuum,” Physical Review E, 48(2), pp. 1562-1565 (1993).
18 – T. W. Barrett, “Tesla’s Nonlinear Oscillator-Shuttle-Circuit (OSC) Theory,” Annales de la Fondation Louis de Broglie, 16(1), pp. 23-41 (1991). Barrett shows that a higher topology EM model (e.g., EM expressed in quaternions) allows shuttling and storage of potentials in circuits, and also allows additional EM functioning of a circuit that a conventional EM analysis cannot reveal. As an example, one may meet optical functioning without the presence of optical materials.