Gravitation and Inertia as a Consequence of Quantum Vacuum Energy
By Dr. Carlos Calvet, hyperspace@telefonica.net ; Francisco Corbera no. 15, E-08360 Canet de Mar (Barcelona), Spain
from Journal of Theoretics Vol.4-2 http://www.journaloftheoretics.com/second-index.htm
# Abstract: By assigning the elementary Planck units to the units of Newtons Gravitational Constant (G), it resulted in G being a function of vacuum (zero point) energy (ZPE). ZPE appears to reduce gravity, as it is inversely proportional to gravitational force. Further, the value of ZPE density-matter equivalent has resulted to be equivalent to the Planck mass in a Planck volume, rendering a much easier way of calculation.
Keywords: Gravity, Gravitational constant, zero point energy, inertia, electrogravity, quantum vacuum.
Introduction:
It was Isaac Newton, who 1687 found first the laws of motion and gravitation. He observed that two masses attract mutually, with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance. The resulting attractive force was in addition always a multiple of this proportionality, being the corresponding constant G (Gravitational Constant), which has an almost constant value of 6.673×10-11 m3kg-1s-2. It has been up to date generally accepted that this natural constant is of unknown origin.
More than 2 centuries later, Max Planck discovered in 1900 that light quanta could explain black body radiation, and thus developed his black body law and his constant. Plancks constant (h) has the value 6,626×10-34 J.s, and represents the smallest energy amount that can exist, demonstrating the real existence of light quanta and overall quantification.
Plancks constant was the starting point for the calculation of some natural units for length, time and mass. Planck showed, simply based on a comparison of units, that by means of G, the speed of light (c) and his constant (h), it is possible to calculate an elementary length, time, and mass, which is now known as Plancks mass, length, and time (mP, lP, tP). The currently accepted values for these Planck units are respectively 2.177×10-8 kg, 1.616×10-35 m, and 5.391×10-44 s, with the latter being in respect to General Relativity, the smallest length and time, space-time can sustain. Intriguing for our purposes was that Plancks units are a function of G (i.e., mP = (h/(2 Pi) c/G)1/2, lP = (h/(2 Pi) G/c3)1/2, tP = (h/(2 Pi) G/c5)1/2 ). This obviously suggested already a century ago, that G is a quantum function.
In 1926, Werner Heisenberg developed the Uncertainty Principle (UP), which was the starting point of a new interpretation of absolute vacuum. According to the UP, a vacuum cannot be completely empty, i.e., it ought to display some background activity in order to allow its own existence. One year later, Paul Dirac described the quantification of electromagnetic fields, creation and annihilation of pairs, virtual particles, and ZPE, suggesting for the first time that an active quantum vacuum (QV) really exists.
On the other hand, H.G.B. Casimir [1], from Dutch Philips Laboratories, discovered in 1948 an attractive force between two very close perfectly conducting plates, which was opposite to the repulsive electric effect of the plates. The force was confirmed and measured precisely by Lamoreux [2]. Milonni et al. [3] showed furthermore that Casimir-plates are being pushed together by the unbalanced ZPE radiation pressure. It seems that this effect derives from the partial shielding of the interior region of the plates from the background ZP fluctuations of the vacuum EM (electromagnetic) field, suggesting again the real existence of a QV and, in addition, of vacuum radiation. Further, B. Haisch, A. Rueda, and H.E. Puthoff deduced for the first time that the inertia of matter could be interpreted at least in part as a reaction force originating in interactions between the EM ZPF and the elementary charged constituents (quarks and electrons) of matter [4]. They also accepted that extensions to include the ZPFs of other fundamental interactions may be necessary for a complete theory of inertia, which suggests in a wider extent that, in addition to Newtons equation of motion (F=m.a), there could be other parameters suitable to being redefined as ZPE-functions [4]. In recent publications [5], [6], H. E. Puthoff and B. Haisch, and A. Rueda calculated respectively the mass-density equivalent of the vacuum ZPF fields (1097 kg/m3) and the maximum energy density, space-time can sustain (10115 J.m-3s-1).
The present paper combines Planck values and the mass-density equivalent of the vacuum ZPF fields with gravity, providing a yet unknown equation, which demonstrates that G is a function of vacuum energy and that this energy weakens mass attraction. Furthermore, new equations for inertia are given and electrogravity in weak gravity shielding experiments is explained as the result of ZPE-manipulation through EM devices.
1. G as a Function of QV-ZPF Mass-Density Equivalent.
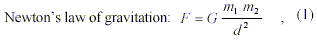
contains the natural constant (G), with almost constant value of 6.673×10-11 m3kg-1s-2. By trying to reveal the meaning of units of G (m3kg-1s-2), we found that they can be best represented by the inverse of mass-density (kg/m3) multiplied by the inverse of square time. In this sense, G can be expressed by the following equation:
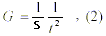
where: S = mass-density (kg/m3), and: t = a certain time (s).
The following step was to assign concrete values to S and t, in order to get the most exact value of G possible. Since G is a universal constant, the most likely is that both, S and t, are themselves constants, so that a medium corresponding to these values had to be found, that is constant in space and time of the whole universe. The only medium that fulfills this condition results to be QV, since it is per definition the most universal medium possible. In addition, the value of S had already been calculated by [5] as the mass-density equivalent of the vacuum ZPE fields (1097 kg/m3).
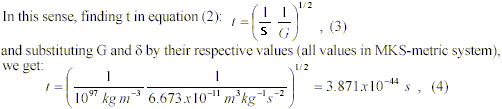
with the result that, t resembles much Planck Time (tP = 5.391×10-44 s).
Since there is no other time that resembles tP so closely, and provided that t is effectively tP, it is legitimate to express G as:
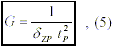
where: S ZP = ZPF mass-density equivalent.
Finding now S ZP in (5), we are able to calculate the exact value of the ZPF mass-density equivalent:
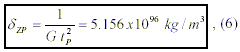
which is almost identical to the1097 kg/m3 that Puthoff[5] calculated for the mass-density equivalent of the vacuum ZPE fields.
# 2. Demonstration that (5) is Correct.
Since the figure of SZP [5] was an approximate value, this author developed an alternative way to demonstrate that (5) is correct. In fact, a QV mass-density can be understood per definition as a Planck mass in a Planck volume:
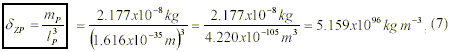
with the values of (6) and (7) being identical to the rounded decimals. The corresponding mean is 5.1575×1096 kg/m3 and in any case, SZP is equal to rounded 5.16×1096 kg/m3. Since (6) and (7) are practically identical, it is legitimate to consider that (5) is a correct equation in describing G.
# 3. Relationship between the ZPF Mass-Density Equivalent and ZPE Density Flow.
Taking Haisch & Ruedas [6] equation of the ZPF energy density flow at the Planck frequency cutoff ( PZP = 2 Pi 2c7/G2 h ) and finding G2, we get:
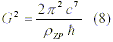
On the other hand, taking equation (5) and substituting tP by its value ( h /(2 Pi) G/c5)1/2), we can find G2:
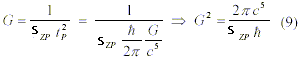
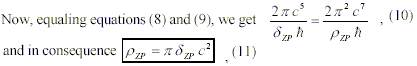
which means that QV energy flow is a function of QV energy density and the speed of light, thus unifying these two apparently different QV-parameters.
# Conclusions and Discussion
1. Gravitation as a Combined Force of Mass Attraction and QV Repulsion
Through (5), Newtons equation of gravitation (1) can be now expressed more precisely (at quantum level) by the following equation:
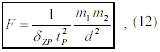
where G has been substituted by a function of QV energy, and S ZP reflects the value of the ZPF mass-density equivalent, which can be now calculated exactly through (6) and/or (7).
Since the left component of (12) is a constant, and the right a variable, they are mutually independent and can be treated separately. In consequence, the first we observe, while regarding equation (12), is that it is composed of two components: a QV (ZPE) component to the left, and a mass attraction component to the right. Secondly, SZP is inversely proportional to gravitational attraction (F), what consequently means in principle that SZP reduces gravity (while mass increases gravity). In consequence, we can call the right component pure mass attraction and the left, vacuum repulsion reaction since mass is obviously the inducing component of gravitation and QV probably reacts (as per the cause-effect principle) to the presence of mutually attracting masses.
In summary, we have found through equation (12) that gravitation is a combined force and that the QV-component (to the left) is opposed to the mutual gravitational attraction of masses (component to the right). The sense of this apparently complex gravitation-generating system in the universe is probably that of stabilizing gravitation, thus avoiding unbiased extreme mass-attractive forces, by opposing a constant reaction effect through QV. If there were no QV in the universe, G would be equal to 1 m3kg-1s-2 (since it would mean that there is no QV reaction) and gravity would be much stronger than it is at present (exactly 6.673×1011 times stronger, since that would be the reverse value of G). In this case, the universe would probably shrink to a spot (Big Crunch), since there would be no effect able to stop a gravitational mass collapse.
2. Gravitational Inertia
Davies [7] and Unruh [8] demonstrated that there exists a real QV-reaction force to accelerated matter, such that mass acceleration and the opposed QV-reaction effect are two forces, which are intimately interrelated in nature, being the corresponding Davies-Unruh effect therefore apparently close to the definition of inertia (a reaction force to acceleration). [7] and [8] demonstrated to a wider extent the link existing between masses and QV.
Since in the macroscopic world, inertia is the immediate reaction effect opposed to acceleration, the left component of eq. (12) is therefore analogous to inertia as it is the reaction force to mass acceleration. In addition, following the above-mentioned principle of independency and treating the left and the right components of eq. (12) independently, gravitation can be redefined as consisting of two components:
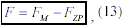
where FM is a pure mass attraction force due to the purely attractive gravitational effect between two masses as if there were no QV (derived from eq. (12) when G = 1 m3kg-1s-2, i.e., G has no effect); FZP is the corresponding decelerating ZPF-reaction force, macroscopically known as inertia; and F is the resulting natural attraction force, which can be measured by man, where G has the known natural value of 6.673×10-11 m3kg-1s-2.
Finding inertia in (13):
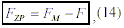
and substituting the above mentioned values of G in (14), while expressing each force in the sense of Newtons gravitation law, we get the value for gravitational inertia:
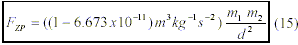
As seen in eq. (15), the value of G for gravitational inertia ((1 – 6.673×10-11) m3kg-1s-2) is very close to 1 (0.99999999993327 m3kg-1s-2) and demonstrates that inertia is a very strong force as expected from its obviously strong decelerating effect on matter in opposition to light (and other photons) that is commonly not decelerated by inertia or by any other similar effect.
Since inertia depends on G, and because according to (5), G is a QV-function, if QV did not exist, there would be no gravitational inertia in the universe, and celestial bodies and masses in general would attract mutually without any control, probably shrinking extremely, since an unbiased mass attraction would possibly make any mass in the universe collapse into small bodies like neutron stars or black holes. QV seems to be therefore a background that guarantees the structural stability of our universe and should furthermore not be manipulated in a global extend without stringent physical control.
3. Non-Gravitational Inertia
For non-mutually attracting bodies, i.e., for individual accelerated objects, (nongravitational) inertia can be derived from (14), by substituting forces through Newtons equation of force (F=ma). For a certain mass, pure mass attraction (FM) is per definition equal to the force, it would produce in the case of the highest acceleration possible, that is, the Planck acceleration (aP=lP/t2P = 5.560×1051 m/s2). In consequence, substituting aP in (14) in the sense of Newtons equation of force, we get:
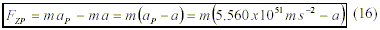
This is inertia of an independent accelerated object of mass m and acceleration a, and shows that inertia of non-gravitational acceleration too limits strongly the independent mass acceleration, as already expected with regard to (15). Eq. (16) predicts correctly the zero inertia of a photon, since in this case, a would be equal to aP (being aP = c/tP, where c = speed of a photon) and FZP = 0.
In consequence, if QV did not exist, there would be no reaction force to non-gravitational acceleration and bodies would reach unbiased velocities in the universe, which probably would not allow the formation of stable celestial bodies as they were always destroyed by heavy collisions with other bodies that would have been violently accelerated by some forces.
In general, without the stabilizing effect of QV, there would be no inertia at all and the universe would obviously be a very chaotic place, where matter collided without any control at very high speeds and unbiased gravitational forces favored the formation of very massive bodies that would carry very high collision energies, thus rendering an almost self-destructive and/or crunching universe that probably could not even exist for more than a single moment.
4. Gravity Control through Electromagnetism
Since G has been proven to be a QV-function by (5), the same applies to gravitation through (12), thus providing the realistic possibility of gravity control through manipulation of ZPE. In fact, (12) demonstrates that QV-energy density weakens gravity. In consequence, if we were able to manipulate ZPE, we would be altering gravity through (12). By increasing QV-energy density, gravity would decrease, while by decreasing the QV-energy density, gravity would increase.
Podkletnov[9] discovered in this sense, in a very controversial work, that a composite bulk YBa2Cu3O7-x superconductor below 70°K under EM field was able to produce, what he called weak gravitation shielding, above and below his superconductor arrangement. The experiment was reproduced by Li et al. [10] and others, and explained by this team, Modanese [11], and others.
According to [10], rotating superconductors in an alternating magnetic field would generate gravity. NASA is studying this effect in its High Temperature Superconductor (HTSC) Research Program, with an aim towards developing technologies for future interstellar navigation.
According to (12), gravity weakens if ZPE increases. Therefore, to produce a gravity shielding effect, the above arrangement should have been able to increase local ZPE density. This could obviously have happened through the involved magnetic fields (superconductor, coils). In order for a magnetic field to be able to increase ZPE, it is necessary that a transfer of photons from the magnetic fields to the ZPF, takes place. If this happened, then the higher concentration of vacuum radiation (photons) around the arrangement would produce a higher radiation pressure on nearby objects, thus lowering their weight as predicted by (12), what was effectively observed by Podkletnov.
In consequence, as (12) shows how gravity could be controlled through ZPE manipulation, Podkletnovs experiment seems to suggest strongly that this happened through EM fields.
Therefore, so-called electrogravity (the unification of gravitation and EM fields) could be achieved directly by combining (12) and electromagnetism in arrangements similar to Podkletnovs.
The driving force that altered gravity would be in the most-simple case, the same well-known vacuum radiation detected in the Casimir-effect [1].
Finally, the main conclusion of this paper is that quantum vacuum is essential for the existence of space-time, so that we cannot imagine space-time without the effects of vacuum radiation. The inclusion of QV in physics provides much clearer equations that tend to simplify each other, even down to a yet unknown extend, with the possibility to get very close to the so-called universal formula. The corresponding much better understanding of the physical world may lead us to unexpected technologies that arise at Planck level such as gravity manipulation, dimensional control, stargate technology, string-colliders etc. [12].
# References
– 1 – H.G.B. Casimir, On the attraction between two perfectly conducting plates, Proc. Kon. Ned. Akad. van Weten., Vol. 51, No. 7, pp. 793-796 (1948).
– 2 – S.K. Lamoreux, Demonstration of the Casimir force in the 0.6 to 6 mm range, Phys. Rev. Lett., Vol. 78, No. 1, pp. 5-8 (1997).
– 3 – P.W. Milonni, R.J. Cook, & M.E. Goggin, Radiation pressure from the vacuum: Physical interpretation of the Casimir force, Phys. Rev. A, Vol. 38, No. 3, pp. 1621-1623 (1988).
– 4 – B. Haisch, A. Rueda & H.E. Puthoff, Inertia as a zero-point-field Lorenz force, Physical Review A, Vol. 49, No. 2, pp. 678-694 (1994).
– 5 – H.E. Puthoff, The Energetic Vacuum: Implications For Energy Research, Speculations in Science and Technology, Vol. 13, No. 4, pp. 247-257 (1990).
– 6 – B. Haisch, A. Rueda, Toward an Interstellar Mission: Zeroing in on the Zero-Point-Field Inertia Resonance, AIP Conference Proceedings of the Space Technology and Applications Forum (STAIF-2000) Conference on Enabling Technology and Required Scientific Developments for Interstellar Missions, January 30-February 3, Albuquerque, NM (2000).
– 7 – P.C.W. Davies, Scalar particle production in Schwarzschild and Rindler metrics, J. Phys. A, Vol. 8, p. 609 (1975).
– 8 – W.G. Unruh, Notes on black-hole evaporation, Phys. Rev. D, Vol. 21, p. 2137 (1980).
– 9 – E.E. Podkletnov (Moscow Chem. Scientific. Ctr.), “Weak Gravitation Shielding Properties of Composite Bulk YBa2Cu3O7-x Superconductor Below 70°K under E.M. Field,” Univ. Cincinnati Engineering, report # MSU-chem 95, abstract cond-mat/9701074, 19 pp. (1997).
– 10 – N. Li, D. Noever, T. Robertson, R. Koczor and W. Brantley, Static Test for A Gravitational Force Coupled to Type II YBCO Superconductors, Physica C, Vol. 281, pp. 260-267 (1997) .
– 11 – G. Modanese, On the theoretical interpretation of E. Podkletnov’s experiment, I.N.F.N. – Trento, Extract from report UTF-391/96, LANL gr-qc/9612022; presented for the World Congress of the International Astronautical Federation, 1997, No. IAA-97-4.1.07.
– 12 – Carlos Calvet, About the quantum vacuum lepton/photon ratio, Journal of Theoretics, Vol. 4, No. 2, April 2002 (preprint)
© Journal of Theoretics, Inc. 2002