### Davis, Eric W.:
## Experimental Concepts for Generating Negative Energy in the Laboratory, from pdf file ‘Eric_Davis.pdf’
by E. W. Davis and H. E. Puthoff ; Inst. for Advanced Studies at Austin, 4030 W. Braker Ln., Ste. 300, Austin, TX 78759, USA ; 512-342-2187, ewdavis@earthtech.org
# Abstract: Implementation of faster-than-light (FTL) interstellar travel via traversable wormholes, warp drives, or other spacetime modification schemes generally requires the engineering of spacetime into very specialized local geometries.
The analysis of these via Einsteins General Theory of Relativity (GTR) field equations plus the resultant equations of state demonstrate that such geometries require the use of exotic matter in order to induce the requisite FTL spacetime modification. Exotic matter is generally defined by GTR physics to be matter that possesses (renormalized) negative energy density, and this is a very misunderstood and misapplied term by the non-GTR community. We clear up this misconception by defining what negative energy is, where it can be found in nature, and we also review the experimental concepts that have been proposed to generate negative energy in the laboratory.
# Keywords: Warp Drive, Traversable Wormholes, General Relativity, Squeezed Quantum States, Electromagnetic Field. PACS: 04.20.Cv, 04.20.Gz, 04.62.+v, 42.50.Dv.
# INTRODUCTION:
It was nearly two decades ago when science fiction media (TV, film and novels) began to adopt traversable wormholes, and more recently stargates, for interstellar travel schemes that allowed their heroes and heroines to travel throughout our galaxy. Little did anyone outside of relativity physics know but that in 1985 physicists M. Morris and K. Thorne at CalTech had in fact discovered the principle of traversable wormholes right out of Einstein’s General Theory of Relativity (GTR, published in 1915). Morris and Thorne (1988) and Morris, Thorne and Yurtsever (1988) did this as an academic exercise, and in the form of problems for a physics final exam, at the request of Carl Sagan who had then completed the draft of his novel Contact. Sagan wanted to follow the genre of what we call science faction, whereby the storys plot would rely on cutting-edge physics concepts to make it more realistic and technically plausible. This little exercise ended up becoming one of the greatest cottage industries in general relativity research the study of traversable wormholes and time machines. Wormholes are hyperspace tunnels through spacetime connecting together either remote regions within our universe or two different universes; they even connect together different dimensions and different times. Space travelers would enter one side of the tunnel and exit out the other, passing through the throat along the way. The travelers would move at
This development was later followed by M. Alcubierres discovery in 1994 of the warp drive spacetime metric, which was another solution to Einsteins GTR field equations. Alcubierre (1994) derived a metric motivated by cosmological inflation that would allow arbitrarily short travel times between two distant points in space. The behavior of the warp drive metric provides for the simultaneous expansion of space behind the spacecraft and a corresponding contraction of space in front of the spacecraft. The warp drive spacecraft would appear to be surfing on a wave of spacetime geometry. A spacecraft can be made to exhibit an arbitrarily large apparent FTL speed (>> c) as viewed by external observers, but its moving local rest frame never travels outside of its local comoving light cone and thus does not violate Special Relativity. A cottage industry of warp drive spacetimes research ensued and papers were published during the next 15 years.
The implementation of FTL interstellar travel via traversable wormholes, warp drives, or other FTL spacetime modification schemes generally requires the engineering of spacetime into very specialized local geometries. The analysis of these via Einsteins GTR field equations plus the resultant equations of state demonstrate that such geometries require the use of exotic matter (or mass-energy) in order to induce the requisite FTL spacetime modification. Exotic matter is generally defined by GTR physics to be matter that possesses (renormalized) negative energy density (sometimes negative stress-tension = positive outward pressure, a.k.a. gravitational repulsion or antigravity), and this is a very misunderstood and misapplied term by the non-GTR community. We clear up this misconception by defining what negative energy is, where it can be found in nature, and we also review the experimental concepts that have been proposed to generate negative energy in the laboratory.
# THE GENERAL RELATIVISTIC DEFINITION OF EXOTIC OR NEGATIVE ENERGY
What is exotic about the matter (or mass-energy) that must be used to generate FTL spacetimes is that it must have negative energy density (Ford and Roman, 2003). The energy density is negative in the sense that the configuration of mass-energy we must deploy to generate and thread a traversable wormhole throat or a warp drive bubble must have an energy density (pE = pc2, p = mass density) that is less than or equal to its stress (t), which is written as: pEE > t. This condition represents one version of what are variously called the weak (WEC), null (NEC), average (AEC), dominant (DEC), and strong (SEC) or standard energy conditions (that are mere hypotheses!), which allegedly forbid negative mass-energy density between material objects to occur in nature. Hawking and Ellis (1973) formulated these energy conditions in order to establish a series of mathematical hypotheses governing the behavior of collapsed-matter singularities in their study of cosmology and black hole physics.
However, there are general theorems of differential geometry that guarantee that there must be a violation of one, some or all of the energy conditions (meaning exotic mass-energy is present) for all FTL spacetimes. With respect to creating FTL spacetimes, negative energy has the unfortunate reputation of alarming physicists. This is unfounded since all the energy condition hypotheses have been experimentally tested in the laboratory and experimentally shown to be false 25 years before their formulation (Visser, 1990 and references cited therein).
For example, the effects of negative energy have been produced in the laboratory via the Casimir Effect and squeezed states of light. Further investigation into this technical issue showed that violations of the energy conditions are widespread for all forms of both classical and quantum matter such as planets, stars, black holes, neutron stars, people, space dust clouds, etc. (Davis, 1999a; Barcelo and Visser, 2002). In addition, Visser (1995) showed that all (generic) spacetime geometries violate all the energy conditions. So the condition that pE > t and/or pE > 0 must be obeyed by all forms of mass-energy in nature is a spurious issue. Violating the energy conditions commits no offense against nature.
Examples of Exotic or Negative Energy
The exotic (energy condition-violating) mass-energy fields that are known to occur in nature are:
– Radial electric or magnetic fields. These are borderline exotic, if their tension were infinitesimally larger, for a given energy density (Herrmann, 1989; Hawking and Ellis, 1973).
– Squeezed quantum states of the electromagnetic field and other squeezed quantum fields; see the following sections for a discussion on squeezed quantum states (Morris and Thorne, 1988; Drummond and Ficek, 2004).
– Gravitationally squeezed vacuum electromagnetic zero-point energy; see the next three sections for the discussion on squeezed quantum states (Hochberg and Kephart, 1991).
– Casimir Effect energy in flat or curved spaces (DeWitt, 1975; Birrell and Davies, 1984; Saunders and Brown, 1991; Milonni, 1994; Milton, 2001).
– Other quantum fields/states/effects. In general, the local energy density in quantum field theory can be negative due to quantum coherence effects (Epstein, Glaser and Jaffe, 1965). Other examples that have been studied are Dirac field states: the superposition of two single particle electron states and the superposition of two multi-electron-positron states (Vollick, 1998; Yu and Shu, 2003). In the former (latter), the energy densities can be negative when two single (multi-) particle states have the same number of electrons (electrons and positrons) or when one state has one more electron (electron-positron pair) than the other.
Since the laws of quantum field theory place no strong restrictions on negative energies and fluxes, then it might be possible to produce gross macroscopic effects such as warp drive, traversable wormholes, violation of the second law of thermodynamics (Ford, 1978; Davies, 1982), and time machines (Morris, Thorne and Yurtsever, 1988; Visser, 1995; Everett, 1996). The above examples are representative forms of mass-energy that possess negative energy density or are borderline exotic. We will explore most of these in what follows.
Squeezed Quantum States
Substantial theoretical and experimental work has shown that in many quantum systems the limits to measurement precision imposed by the quantum vacuum zero-point fluctuations (ZPF) can be breached by decreasing the noise in one observable (or measurable quantity) at the expense of increasing the noise in the conjugate observable; at the same time the variations in the first observable, say the energy, are reduced below the ZPF such that the energy becomes negative. Squeezing is thus the control of quantum fluctuations and corresponding uncertainties, whereby one can squeeze the variance of one (physically important) observable quantity provided the variance in the (physically unimportant) conjugate variable is stretched/increased. The squeezed quantity possesses an unusually low variance, meaning less variance than would be expected on the basis of the equipartition theorem. One can in principle exploit quantum squeezing to extract energy from one place in the ordinary vacuum at the expense of accumulating excess energy elsewhere (Morris and Thorne, 1988).
Squeezed Light
The squeezed state of the electromagnetic field is one of the numerous examples where quantum fields can have negative energy density. Such a state became a physical reality in the laboratory (Slusher et al., 1985; Slusher and Yurke, 1986; Robinson, 1985; 1986) as a result of the nonlinear-optics technique of squeezing, i.e., of moving some of the quantum-fluctuations of laser light out of the cos w (t – z/c) part of the beam and into the sin w (t – z/c) part. This pertains to a particular electric field mode of coherent light from an ideal laser: E = E0[Acos w (t z/c) + Bsin w (t z/c)], where the electric field amplitude E0is constant, w is the angular frequency, z is the beam propagation direction, t is time, and (A, B) are the field quadrature operators corresponding to the quantized harmonic oscillator (i.e., the single-mode electromagnetic field) position and momentum, respectively. A and B are defined to be: 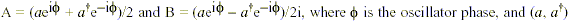 are the usual annihilation and creation operators. A and B are the observables we are interested in and they must obey the commutation relation: [A,B] = ih/2, where h is Plancks reduced constant. The operators (a,a+) also obey the commutation relation: [a,a+] = 1. And the oscillator vacuum is defined in the usual way: a|vac> = 0 (i.e., a annihilates the vacuum state |vac>). The corresponding uncertainty relation
are the usual annihilation and creation operators. A and B are the observables we are interested in and they must obey the commutation relation: [A,B] = ih/2, where h is Plancks reduced constant. The operators (a,a+) also obey the commutation relation: [a,a+] = 1. And the oscillator vacuum is defined in the usual way: a|vac> = 0 (i.e., a annihilates the vacuum state |vac>). The corresponding uncertainty relation 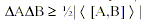 has one built-in degree of freedom: one can squeeze the variance of one observable provided the variance in the conjugate observable is stretched. (Note: the signifies taking the absolute value or magnitude of the expectation value of the enclosed quantity.) Squeezing becomes important when
has one built-in degree of freedom: one can squeeze the variance of one observable provided the variance in the conjugate observable is stretched. (Note: the signifies taking the absolute value or magnitude of the expectation value of the enclosed quantity.) Squeezing becomes important when 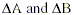 are limited by the minimized uncertainty product:
are limited by the minimized uncertainty product: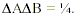 The observable that gets squeezed will have its fluctuations reduced below the vacuum ZPF.
The observable that gets squeezed will have its fluctuations reduced below the vacuum ZPF.
See Drummond and Ficek (2004) for a comprehensive review of the theoretical and experimental state-of-the-art on squeezed light physics.
To squeeze, one acts on a (complex) state X using a squeeze operator, S(X), for a single quantized harmonic oscillator: S(X) = exp[½(Xa2 – X+ a+2)] (note: X+ signifies the complex conjugate of X). The state X = reiS determines the size of the squeezing, where r is the amplitude (giving a measure of the mean photon number in X) and S is the phase of squeezing. The squeezed vacuum is therefore defined as: 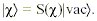 Calculating the uncertainties
Calculating the uncertainties  with respect to the squeezed vacuum gives
with respect to the squeezed vacuum gives  therefore DeltaB is squeezed and DeltaA is stretched. Thus S(X) reduces the uncertainty in B and increases that in A while maintaining the minimized uncertainty product. The act of squeezing transforms the phase space circular noise profile characteristic of the vacuum into an ellipse, whose semimajor and semiminor axes are given by
therefore DeltaB is squeezed and DeltaA is stretched. Thus S(X) reduces the uncertainty in B and increases that in A while maintaining the minimized uncertainty product. The act of squeezing transforms the phase space circular noise profile characteristic of the vacuum into an ellipse, whose semimajor and semiminor axes are given by 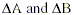 , respectively. This applies to coherent states in general, and the usual vacuum is also a coherent state with eigenvalue zero. As this ellipse rotates about the origin with angular frequency w, these unequal quadrature uncertainties manifest themselves in the oscillator energy by periodic occurrences, which are separated by one quarter cycle, of both smaller and larger fluctuations compared to the unsqueezed vacuum.
, respectively. This applies to coherent states in general, and the usual vacuum is also a coherent state with eigenvalue zero. As this ellipse rotates about the origin with angular frequency w, these unequal quadrature uncertainties manifest themselves in the oscillator energy by periodic occurrences, which are separated by one quarter cycle, of both smaller and larger fluctuations compared to the unsqueezed vacuum.
If one squeezes the vacuum, i.e., if one puts vacuum rather than laser light into the input port of a squeezing device, then one gets at the output an electromagnetic field with weaker fluctuations and thus less energy density than the vacuum at locations where 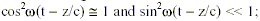 but with greater fluctuations and thus greater energy density than the vacuum at locations where
but with greater fluctuations and thus greater energy density than the vacuum at locations where 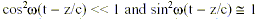 (Caves, 1981; Morris and Thorne, 1988). Since the vacuum is defined to have vanishing energy density, any region with less energy density than the vacuum actually has a negative (renormalized) expectation value for the energy density. Therefore, a squeezed vacuum state consists of a traveling electromagnetic wave that oscillates back and forth between negative energy density and positive energy density, but has positive time-averaged energy density.
(Caves, 1981; Morris and Thorne, 1988). Since the vacuum is defined to have vanishing energy density, any region with less energy density than the vacuum actually has a negative (renormalized) expectation value for the energy density. Therefore, a squeezed vacuum state consists of a traveling electromagnetic wave that oscillates back and forth between negative energy density and positive energy density, but has positive time-averaged energy density.
Gravitationally Squeezed Electromagnetic ZPF
A natural source of negative energy comes from the effect that gravitational fields (of astronomical bodies) in space have upon the surrounding vacuum. For example, the gravitational field of the Earth produces a zone of negative energy around it by dragging some of the virtual particle pairs (a.k.a. vacuum ZPF) downward. This concept was initially developed in the 1970s as a byproduct of studies on quantum field theory in curved space (Birrell and Davies, 1982). However, Hochberg and Kephart (1991) derived an important application of this concept to the problem of creating and stabilizing traversable wormholes, and their work was corrected and extended by Davis (1999b). They proved that one can utilize the negative vacuum energy densities, which arise from distortion of the electromagnetic zero point fluctuations due to the interaction with a prescribed gravitational background, for providing a violation of the energy conditions.
Hochberg and Kephart (1991) showed that the squeezed quantum states of quantum optics provide a natural form of matter having negative energy density. The analysis, via quantum optics, shows that gravitation itself provides the mechanism for generating the squeezed vacuum states needed to support stable traversable wormholes. The production of negative energy densities via a squeezed vacuum is a necessary and unavoidable consequence of the interaction or coupling between ordinary matter and gravity, and this defines what is meant by gravitationally squeezed vacuum states. The magnitude of the gravitational squeezing of the vacuum can be estimated from the quantum optics squeezing condition for given transverse momentum and (equivalent) energy eigenvalues (j) of two electromagnetic ZPF field modes, such that this condition is subject to 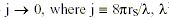 is the ZPF mode wavelength, and rS is the Schwarzschild radius of the astronomical body (or mass) in question (Hochberg and Kephart, 1991; Davis, 1999b). (Note: rS is only a convenient radial distance parameter for each body/mass under examination and there is no black hole collapse involved in this analysis. The Schwarzschild radius is the critical radius, according to GTR, at which a spherically symmetric massive body becomes a black hole, i.e. at which light is unable to escape from the bodys surface. We can actually choose any radial distance from the body/mass in question to perform this analysis, but using rS makes the equations simpler in form.) This squeezing condition simply states that substantial gravitational squeezing of the vacuum occurs for those ZPF field modes with
is the ZPF mode wavelength, and rS is the Schwarzschild radius of the astronomical body (or mass) in question (Hochberg and Kephart, 1991; Davis, 1999b). (Note: rS is only a convenient radial distance parameter for each body/mass under examination and there is no black hole collapse involved in this analysis. The Schwarzschild radius is the critical radius, according to GTR, at which a spherically symmetric massive body becomes a black hole, i.e. at which light is unable to escape from the bodys surface. We can actually choose any radial distance from the body/mass in question to perform this analysis, but using rS makes the equations simpler in form.) This squeezing condition simply states that substantial gravitational squeezing of the vacuum occurs for those ZPF field modes with 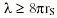 of the mass in question (whose gravitational field is squeezing the vacuum).
of the mass in question (whose gravitational field is squeezing the vacuum).
The general result of the gravitational squeezing effect is that as the gravitational field strength increases, the negative energy zone (surrounding the mass) also increases in strength. Table 1 shows when gravitational squeezing becomes important for example masses. The table shows that in the case of the Earth, Jupiter and the Sun, thissqueeze effect is extremely feeble because only ZPF mode wavelengths above 0.2 m 78 km are affected. For a solar mass black hole (radius of 2.95 km), the effect is still feeble because only ZPF mode wavelengths above 78 km are affected. But also note in the table that Planck mass objects will have an enormously strong negative energy zone surrounding them because all ZPF mode wavelengths above 8.50 x 10-34 meters will be squeezed, in other words, all wavelengths of interest for vacuum fluctuations. Protons will have the strongest negative energy zone in comparison because the squeezing effect includes all ZPF mode wavelengths above 6.50 x 10 -53 meters.
Furthermore, a body smaller than a nuclear diameter ( +-10-16 m) and containing the mass of a mountain (+- 1011 kg) has a fairly strong negative energy zone because all ZPF mode wavelengths above 10 15 meters will be squeezed.

We are presently unaware of any way to artificially generate gravitational squeezing of the vacuum in the laboratory. This will be left for future investigation.
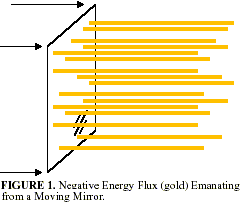
A Moving Mirror
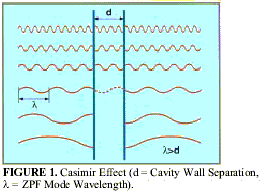
Negative energy can be created by a single moving reflecting surface (a moving mirror), see Figure 1. A mirror moving with increasing acceleration generates a flux of negative energy that emanates from its surface and flows out into the space ahead of the mirror (Birrell and Davies, 1984; Walker, 1985). However, this effect is known to be exceedingly small, and it is not the most effective way to generate negative energy for our purposes. We will not consider this scheme any further.
# PROPOSED EXPERIMENTS FOR GENERATING NEGATIVE ENERGY
In what follows we outline five proposed experiments for generating negative energy in the lab. A detailed technical/engineering analysis of each of these is the subject of future work, and space limits the amount of technical detail that can be provided in this paper.
Negative Casimir Energy
The Casimir Effect is by far the easiest and most well known way to generate negative energy in the lab. The energy density 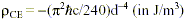 within a Casimir cavity is negative and manifests itself by producing a force of attraction between the cavity walls (d is the wall separation). This has been measured in the lab to a very high level of precision for a number of different cavity geometries (see Milton, 2001 and the references cited therein). But cavity dimensions must be made exceedingly small in order to generate a significant amount of negative energy for our purposes. In order to use the Casimir Effect to generate a spherically symmetric traversable wormhole throat of radius rwh, we will need to design a cavity of perfectly conducting spherically concentric thin plates with a plate separation of (Morris, Thorne and Yurtsever, 1988):
within a Casimir cavity is negative and manifests itself by producing a force of attraction between the cavity walls (d is the wall separation). This has been measured in the lab to a very high level of precision for a number of different cavity geometries (see Milton, 2001 and the references cited therein). But cavity dimensions must be made exceedingly small in order to generate a significant amount of negative energy for our purposes. In order to use the Casimir Effect to generate a spherically symmetric traversable wormhole throat of radius rwh, we will need to design a cavity of perfectly conducting spherically concentric thin plates with a plate separation of (Morris, Thorne and Yurtsever, 1988):
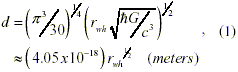
where G is the Universal Gravitation Constant and rwh is in meters. Equation (1) shows that a 1 km radius throat will require a cavity plate separation of 1.28 x 10-16 m (smaller than a nuclear diameter), and the energy density (pEC) generated by this configuration is -4.83 x 1036 J/m3. In contrast, a wormhole with a throat radius of 1 AU (mean Earth-Sun distance) will require a plate separation of 1.57 x 10-12 m (35% smaller than the electrons Compton wavelength), and generate -2.16 x 1020 J/m3 of energy density. There is no technology known today that can engineer a cavity with such miniscule plate separations. In addition, such miniscule plate separations are unrealistic because the Casimir Effect switches over into the non-retarded field behavior (~ d-3) of van der Waals forces when plate separations go below the wavelength (15 nm) where they are no longer perfectly conducting (Forward, 1983). We will consider this scheme no further.
# Radial Electric/Magnetic Fields
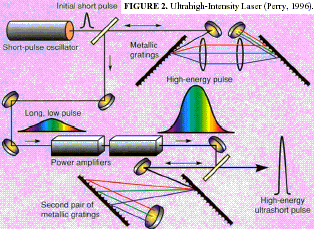
It is beyond the scope of this paper to include all the technical configurations by which one can generate radial electric or magnetic fields. Suffice it to say that ultrahigh-intensity tabletop lasers have been used to generate extreme electric and magnetic field strengths in the lab. Ultrahigh-intensity lasers use the chirped-pulse amplification (CPA) technique to boost the total output beam power. All laser systems simply repackage energy as a coherent package of optical power, but CPA lasers repackage the laser pulse itself during the amplification process. In typical high-power short-pulse laser systems, it is the peak intensity, not the energy or the fluence, which causes pulse distortion or laser damage. However, the CPA laser dissects a laser pulse according to its frequency components, and reorders it into a time-stretched lower-peak-intensity pulse of the same energy (Perry, 1996; 2000; Mourou, Barty and Perry, 1998). This benign pulse can then be amplified safely to high energy, and then only afterwards reconstituted as a very short pulse of enormous peak power a pulse which could never itself have passed safely through the laser system (see Figure 2). Made more tractable in this way, the pulse can be amplified to substantial energies (with orders of magnitude greater peak power) without encountering intensityrelated problems.
The extreme output beam power, fields and physical conditions that have been achieved by ultrahigh-intensity tabletop lasers are (Mourou, Barty and Perry, 1998):
– Power Intensity 1015 1026 Watts cm2 (1030 W/cm2using SLAC as a booster)
– Peak Power Pulse 3femtoseconds
– E-fields +- 1014 1018 V/m [note: the critical quantum-electrodynamical (vacuum breakdown) field strength is Ec = 2me2 c3/he +- 1018 V/m; me and e are the electron mass and charge]
– B-fields +- several x 106 Tesla [note: the critical quantum-electrodynamical (vacuum breakdown) field strength is Bc = Ec/c +- 1010 Tesla]
– Ponderomotive Acceleration of Electrons +- 1017 1030 gs (1 g = 9.81 m/sec2)
– Light Pressure +- 109 1015 bars
– Plasma Temperatures > 1010 K
We find from the above data that ultrahigh-intensity lasers can generate an electric field energy density of ~ 1016 1028 J/m3 and a magnetic field energy density of ~ 1019 J/m3. These energy densities are about the right order of magnitude to explore generating kilometer to AU sized wormholes. But that would be difficult to engineer on Earth.
However, these energy densities are well above what would be required to explore the generation of microwormholes in the lab.
# Negative Energy from Squeezed Light
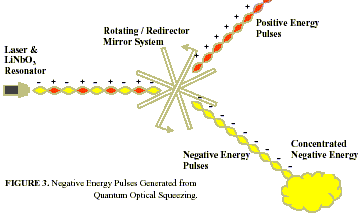
Negative energy can be generated by an array of ultrahigh intensity (femtosecond) lasers using an ultrafast rotating mirror system. In this scheme (originally due to Davies, 2001) a laser beam is passed through an optical cavity resonator made of lithium niobate (LiNbO3) crystal that is shaped like a cylinder with rounded silvered ends to reflect light. The resonator will act to produce a secondary lower frequency light beam in which the pattern of photons is rearranged into pairs. This is the quantum optical squeezing of light effect that we described previously.
Therefore, the squeezed light beam emerging from the resonator will contain pulses of negative energy interspersed with pulses of positive energy in accordance with the quantum squeezing model (see Figure 3).
In this example both the negative and positive energy pulses are of +- 10-15 second duration. We could arrange a set of rapidly rotating mirrors to separate the positive and negative energy pulses from each other. The light beam is to strike each mirror surface at a very shallow angle while the rotation ensures that the negative energy pulses are reflected at a slightly different angle from the positive energy pulses. A small spatial separation of the two different energy pulses will occur at some distance from the rotating mirror. Another system of mirrors will be needed to redirect the negative energy pulses to an isolated location and concentrate them there.
The rotating mirror system can actually be implemented via non-mechanical means. A chamber of sodium gas is placed within the squeezing cavity, and a laser beam is directed through the gas. The beam is reflected back on itself by a mirror to form a standing wave within the sodium chamber. This wave causes rapid variations in the optical properties of the sodium thus causing rapid variations in the squeezed light so that we can induce rapid reflections of pulses by careful design (Slusher and Yurke, 1986).
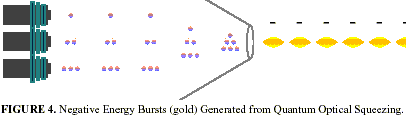
Another way to squeeze light would be to manufacture extremely reliable light pulses containing precisely one, two, three, etc. photons apiece and combine them together to create squeezed states to order. Davies (2001) points out that superimposing many such states could theoretically produce bursts of intense negative energy (see Figure 4).
Photonic crystal research has already demonstrated the feasibility of using photonic crystal waveguides (mixing together the classical and quantum properties of optical materials) to engineer light sources that produce beams containing precisely one, two, three, etc., photons. For example, researchers at Melbourne University used a microwave oven to fuse a tiny diamond, just 1/1000th of a millimeter, onto an optical fiber, which could be used to create a single photon beam of light (Rabeau et al., 2004a; 2004b). The combining of different beams containing different (finite integer) number of photons is already state-of-the-art practice via numerous optical beam combining methods that can readily be extended to our application.
For the squeezed (electromagnetic) vacuum state, the energy density is given by (Pfenning, 1998):
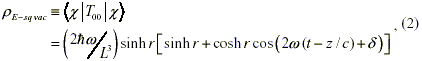
where L3 is the volume of a large box with sides of length L (i.e., we put the quantum field in a box with periodic boundary conditions), and T00 is the energy density component of the stress-energy tensor. Equation (2) shows that the energy density falls below zero once every cycle when the condition cosh r > sinh r is met. It turns out that this is always true for every nonzero value of r, so the energy density becomes negative at some point in the cycle for a general squeezed vacuum state. On another note, when a quantum state is close to a squeezed vacuum state, there will almost always be some negative energy densities present, and the fluctuations in start to become nearly as large as the expectation value itself.
# Observing Negative Energy in the Lab
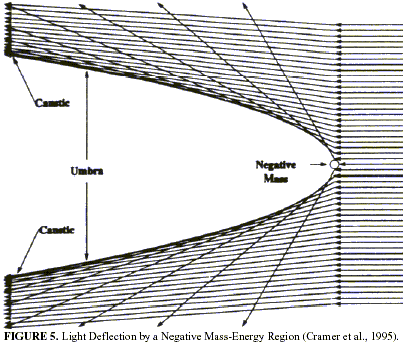
Negative energy should be observable in lab experiments. The presence of naturally occurring negative energy regions in space is predicted to produce a unique signature corresponding to lensing, chromaticity and intensity effects in micro- and macro-lensing events on galactic and extragalactic/cosmological scales (Cramer et al., 1995; Torres, Anchordoqui and Romero, 1998; Torres, Romero and Anchordoqui, 1998; Anchordoqui et al., 1999; Safonova, Torres and Romero, 2001; Eiroa, Romero and Torres, 2001). It has been shown that these effects provide a specific signature that allows for discrimination between ordinary (positive mass-energy) and negative massenergy lenses via the spectral analysis of astronomical lensing events. Theoretical modeling of negative energy lensing effects has led to intense astronomical searches for naturally occurring traversable wormholes in the universe (see above references). Computer model simulations and comparison of their results with recent satellite observations of gamma ray bursts (GRBs) has shown that putative negative energy (i.e., traversable wormhole) lensing events very closely resembles the main features of some GRBs. Visser (1997) also points out that current observational data suggests that large amounts of naturally occurring exotic mass-energy must have existed sometime between the epoch of galaxy formation and the present in order to (properly) quantitatively account for the age-of-the-oldest-stars-in-the-galactic halo problem and the cosmological evolution parameters.
When background light rays strike a negative energy lensing region, they are swept out of the central region thus creating an umbra region of zero intensity. At the edges of the umbra the rays accumulate and create a rainbow-like caustic with enhanced light intensity (see Figure 5). The lensing of a negative mass-energy region is not analogous to a diverging lens because in certain circumstances it can produce more light enhancement than does the lensing of an equivalent positive mass-energy region. Real background sources in lensing events can have non-uniform brightness distributions on their surfaces and a dependency of their emission with the observing frequency. These complications can result in chromaticity effects, i.e. in spectral changes induced by differential lensing during the event. The modeling of such effects is quite lengthy, somewhat model dependent, and with recent application only to astronomical lensing events. Suffice it to say that future work is necessary to scale down the predicted lensing parameters and characterize their effects for lab experiments in which the negative energy will not be of astronomical magnitude. Present ultrahigh-speed optics and optical cavities, lasers, photonic crystal (and switching) technology, sensitive nano-sensor technology, and other techniques are very likely capable of detecting the very small magnitude lensing effects expected in lab experiments.
# The Quantum Inequalities
The Quantum Inequalities (QI) conjecture is an ad hoc extension of the Heisenberg Uncertainty Principle. They were essentially derived by a small group of curved spacetime quantum field theory specialists for the purpose of making the universe look rational and uninteresting (Pfenning, 1998; see also the excellent review by Ford and Roman, 2003). A small cottage industry of research papers has sprouted up on this one topic alone. The literature is too numerous to cite here. This small group is prejudiced against faster-than-light motion, traversable wormhole and warp drive spacetimes, time machines, negative energy, and other related issues having to do with the violation of the second law of thermodynamics. This group accepts the reality of the theoretical and proven experimental existence of negative energy density and fluxes, but they dont accept the consequences of its various manifestations in spacetime.
The QI supposedly relates the energy density of a free quantum field and the time during which this energy density is observed. When generating negative energy via squeezed quantum states the QI postulates that: a) the longer the pulse of negative energy lasts, the weaker it must be, b) a pulse of positive energy must follow and the magnitude of the positive pulse must exceed that of the initial negative pulse, c) the longer the time interval between the two pulses, the larger the positive pulse must be. This actually sounds quite reasonable on energy conservation grounds until one finds out that the Casimir Effect (a squeezed vacuum state by virtue of its cavity boundary conditions) violates all three conditions. The Casimir Effect even violates a steady-state QI analysis. Squeezed light was also shown to violate the above postulates. Visser (1997) points out that observational data indicates that large amounts of exotic mass-energy is required to exist in the universe in order to account for the observed cosmological evolution parameters. The QI have thus not been verified by laboratory experiments or observational data. The assumptions used to derive the QI and the efficacy of the derivations for various cases has been called into question by numerous investigators. Krasnikov (2004) constructed an explicit counterexample for generalized FTL spacetimes showing that the relevant QI does not hold. Therefore, we will ignore the QI conjecture.
# CONCLUSION
We reviewed the general relativistic definition of negative energy and identified the forms of negative energy that are known to occur in nature or have been predicted to occur. We examined each of these and characterized their physics and the magnitude of negative energy they are capable of producing. Next we reviewed first-order experimental concepts that we believe will achieve the objective of generating negative energy in the lab. It was demonstrated that radial electric or magnetic fields generated by ultrahigh-intensity lasers are capable of achieving energy densities large enough to observe laboratory-scale spacetime effects. It was also shown that the negative energy densities generated by squeezed quantum state processes are capable of generating negative energy.
However, future work is needed to establish the experimental parameters required to specifically separate out the negative energy pulses from the positive energy pulses in optical cavity systems at ultrahigh speed. The astronomical observation of naturally occurring negative energy lensing events has been predicted. The predicted lensing effects have been characterized and quantified but this also needs to be done for laboratory-scale experiments, and this will be the subject of future work. Last, the Quantum Inequalities conjecture is predicted to impose serious constraints on the amount of negative energy that can be generated and utilized. However, this has been disproved to some extent for a variety of spacetimes and quantum field cases. There is also experimental evidence that contradicts the main postulates and assumptions of the QI conjecture.
# ACKNOWLEDGMENTS
We would like to thank the Institute for Advanced Studies at Austin for supporting this work. This work previously originated under Air Force Research Laboratory (AFMC) contract F04611-99-C-0025. We also wish to extend our thanks and appreciation to Frank Mead (AFRL/PRSP, Edwards AFB, CA), members of the Air Staff (Air Force HQ, Pentagon), and Paul Murad (Department of Defense) for encouraging us to explore this topic.
# REFERENCES
– Alcubierre, M., The warp drive: hyper-fast travel within general relativity, Class. Quant. Grav. 11, L73-L77 (1994).
– Anchordoqui, L. A., et al., In Search for Natural Wormholes, Mod. Phys. Lett. A 14, 791-797 (1999).
– Barcelo, C., and Visser, M., Twilight for the energy conditions?, Int. J. Mod. Phys. D 11, 1553 (2002).
– Birrell, N. D., and Davies, P. C. W., Quantum fields in curved space, Cambridge University Press, Cambridge, 1984.
– Caves, C. M., Quantum-mechanical noise in an interferometer, Phys. Rev. D 23, 1693-1708 (1981).
– Cramer, J. G., et al., Natural wormholes as gravitational lenses, Phys. Rev. D 51, 3117-3120 (1995).
– Davies, P. C. W., Can moving mirrors violate the second law of thermodynamics?, Phys. Lett. B 11, 215 (1982).
– Davies, P. C. W., How to Build a Time Machine, Penguin Books, New York, 2001.
– Davis, E. W., Research Summary Report #2 to Dr. Hal Puthoff, IASA: Brief Summary of Gravitational Vacuum Polarization. Parts I IV, NASA Research Center Online Library Interstellar Studies (1999a).
– Davis, E. W., Research Summary Report #1 to Dr. Hal Puthoff, IASA: Brief Summary of Lorentzian Wormholes from the Gravitationally Squeezed Vacuum, NASA Research Center Online Library Interstellar Studies (1999b).
– Davis, E. W., Teleportation Physics Study, Final Report AFRL-PR-ED-TR-2003-0034, Air Force Research Laboratory, Air Force Materiel Command, Edwards AFB, CA, 2004, pp. 3-11.
– DeWitt, B. S., Quantum Field Theory in Curved Spacetime, Phys. Lett. C 19, 295-357 (1975).
– Drummond, P. D., and Ficek, Z. (eds.), Quantum Squeezing, Springer-Verlag, Berlin, 2004.
– Eiroa, E., Romero, G. E., and Torres, D. F., Chromaticity Effects in Microlensing by Wormholes, Mod. Phys. Lett. A 16, 973-983 (2001).
– Epstein, H., Glaser, V., and Jaffe, A., Nonpositivity of the Energy Density in Quantized Field Theories, Nuovo Cimento 36, 1016-1022 (1965).
– Everett, A. E., Warp drive and causality, Phys. Rev. D 53, 7365-7368 (1996).
– Ford, L. H., Proc. Roy. Soc. London A364, 227 (1978).
– Ford, L. H., and Roman, T. A., Negative Energy, Wormholes and Warp Drive, Sci. Am. 13, 84-91 (2003).
– Forward, R. L., Alternate Propulsion Energy Sources, Final Report AFRPL TR-83-067, Air Force Rocket Propulsion Laboratory, Air Force Space Tech. Ctr. Space Div., Air Force Systems Command, Edwards AFB, CA, 1983, pp. A1-A14.
– Hawking, S. W., and Ellis, G. F. R., The Large-Scale Structure of Space-Time, Cambridge Univ. Press, Cambridge, 1973, pp. 88-91, 95-96.
– Herrmann, F., Energy Density and Stress: A New Approach to Teaching Electromagnetism, Am. J. Phys. 57, 707-714 (1989).
– Hochberg, D., and Kephart, T. W., Lorentzian wormholes from the gravitationally squeezed vacuum, Phys. Lett. B 268, 377- 383 (1991).
– Krasnikov, S., Counter example to a quantum inequality, arxiv.org/gr-qc/0409007 (2004).
– Milonni, P. W., The Quantum Vacuum: An Introduction to Quantum Electrodynamics, Academic Press, New York, 1994.
– Milton, K. A., The Casimir Effect: Physical Manifestations of Zero-Point Energy, World Scientific, New Jersey, 2001.
– Morris, M. S., and Thorne, K. S., Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity, Am. J. Phys. 56, 395-412 (1988).
– Morris, M. S., Thorne, K. S., and Yurtsever, U., Wormholes, time machines, and the weak energy conditions, Phys. Rev. Lett. 61, 1446-1449 (1988).
– Mourou, G. A., Barty, C. P. J., and Perry, M. D., Ultrahigh-Intensity Lasers: Physics Of The Extreme On A Tabletop, Physics Today 51, 22-28 (1998).
– Perry, M. D., Crossing the Petawatt Threshold, Science & Technology Review (LLNL-DoE publ.), 4-11 (December 1996).
– Perry, M. D., The Amazing Power of the Petawatt, Science & Technology Review (LLNL-DoE publ.), 4-12 (March 2000).
– Pfenning, M. J., Quantum Inequality Restrictions on Negative Energy Densities in Curved Spacetimes, Ph.D. Dissertation, Tufts Univ., Medford, MA, 1998 (arxiv.org/gr-qc/9805037).
– Rabeau, J. R., et al., Fabrication of single nickel-nitrogen defects in diamond by chemical vapor deposition, arxiv.org/condmat/ 0411245 (2004a).
– Rabeau, J. R., et al., Diamond chemical vapor deposition on optical fibers for fluorescence waveguiding, arxiv.org/condmat/ 0411249 (2004b).
– Robinson, A. L., Bell Labs Generates Squeezed Light, Science 230, 927-929 (1985).
– Robinson, A. L., Now Four Laboratories Have Squeezed Light, Science 233, 280-281 (1986).
– Safonova, M., Torres, D. F., and Romero, G. E., Macrolensing Signatures of Large-Scale Violations of the Weak Energy Condition, Mod. Phys. Lett. A 16, 153-162 (2001).
– Saunders, S., and Brown, H. R. (eds.), The Philosophy of Vacuum, Clarendon Press, Oxford, 1991.
– Slusher, R. E., et al., Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity, Phys. Rev. Lett. 55, 2409-2412 (1985).
– Slusher, R. E., and Yurke, B., Squeezed Light, Sci. Am. 254, 50-56 (1986).
– Torres, D. F., Anchordoqui, L. A., and Romero, G. E., Wormholes, Gamma Ray Bursts and the Amount of Negative Mass in the Universe, Mod. Phys. Lett. A 13, 1575-1581 (1998).
– Torres, D. F., Romero, G. E., and Anchordoqui, L. A., Might some gamma ray bursts be an observable signature of natural wormholes, Phys. Rev. D 58, 123001:1-8 (1998).
– Visser, M., Wormholes, baby universes, and causality, Phys. Rev. D 41, 1116-1124 (1990).
– Visser, M., Lorentzian Wormholes: From Einstein to Hawking, AIP Press, New York, 1995.
– Visser, M., Energy Conditions in the Epoch of Galaxy Formation, Science 276, 88-90 (1997).
– Vollick, D. N., Negative energy density states for the Dirac field in flat spacetime, Phys. Rev. D 57, 3484-3488 (1998).
– Walker, W. R., Negative energy fluxes and moving mirrors in curved space, Class. Quant. Grav. 2, L37-L40 (1985).
– Yu, H., and Shu, W., Quantum states with negative energy density in the Dirac field and quantum inequalities, Phys. Lett. B 570, 123-128 (2003).
## Review of Experimental Concepts for Studying the Quantum Vacuum Field, from pdf file ‘Davis_STAIF06.pdf’
E.W. Davis1, V.L. Teofilo2, B. Haisch3, H.E. Puthoff1, L.J. Nickisch4, A. Rueda5, and D.C. Cole6
1 Inst. for Advanced Studies at Austin, 4030 W. Braker Ln., Ste. 300, Austin, TX 78759, USA
2 Lockheed Martin Space Systems, M.S. L2-01/B157, PO Box 3504, Sunnyvale, CA 94089, USA
3 ManyOne Networks, 100 Enterprise Way, Bldg. G-370, Scotts Valley, CA 95066, USA
4 NorthWest Research Associates, 14508 NE 20th St., Bellevue, WA 98007, USA
5 Dept. of Electrical Engineering, ECS Bldg., Cal. State Univ.-Long Beach, Long Beach, CA 90840, USA
6 Dept. of Manufacturing Engineering, Boston University, 15 St. Marys Street, Boston, MA 02215, USA
1 512-342-2187, ewdavis@earthtech.org
# Abstract: We review concepts that provide an experimental framework for exploring the possibility and limitations of accessing energy from the space vacuum environment. Quantum electrodynamics (QED) and stochastic electrodynamics (SED) are the theoretical approaches quiding this experimental investigation. This investigation expolres the question of whether the quantum vacuum field contains useful energy that can be exploited for applications under the action of a catalyst, or cavity structure, so that energy conservation is not violated. This is similar to the same technical problem at about the same level of technology as that faced by early nuclear energy pioneers who searched for, and successfully discovered, the unique material structure that caused the release of nuclear energy via the neutron chain reaction.
# Keywords: Zero-point Fluctuations, Quantum Vaccum, Quantum Electrodynamics, Stochastic Electrodynamics.
PACS: 03.50.De, 05.10.Gg, 12.20. m.
# Introduction:
Quantum theory predicts that the vacuum of space in the universe is filled with low-energy electromagnetic waves, random in phase and amplitude and propagating in all possible directions. This is different from the cosmic microwave background radiation and it is referred to as the electromagnetic quantum vacuum since it is the lowest state of otherwise empty space. When integrated over all frequency modes up to the Planck frequency, VP (~ 1043 Hz), this represents an enormous potential source of energy with a density of as much as ~ 10113 J/m3 which is far in excess of any other known energy source even if only an infinitesimal fraction of it is accessible. This is also several tens of orders of magnitude greater than the energy density of matter-antimatter annihilation reactions. Even if we are constrained to integrate over all frequency modes only up to the nucleon Compton frequency (~ 1023 Hz), this energy density will still be enormous (~ 1035 J/m3). And we have not taken into account the fact that the electromagnetic quantum vacuum is not alone by itself. On the contrary, it intimately couples to the charged particles in the Dirac sea of particle-antiparticle pairs and thereby couples to the other interactions of the Standard Model (weak and strong force vacua). So all the numbers we just mentioned admit of some further adjustment.
This energy is so enormous that most physicists believe that even though zero-point energy (ZPE) seems to be an inescapable consequence of quantum field theory, it cannot be physically real, and so is subtracted away in calculations by ad hoc means. A minority of physicists do, however, accept it as a real energy which we cannot directly sense since it is the same everywhere, even inside our bodies and measuring devices. From this perspective, the ordinary world of matter and energy is like foam atop the quantum vacuum sea. It does not matter to a ship how deep the ocean is below it. If the ZPE is real, then there is the possibility that it can be tapped as a source of power or be harnessed to generate a propulsive force for space travel.
The propeller or the jet engine of an aircraft can push air backwards to propel the aircraft forward. A ship or boat propeller does the same thing in water. On Earth there is always air or water available to push against. Ignoring mass fluctuations or other propellant concepts, a rocket in space has nothing to push against, and so it needs to carry propellant to eject in the absence of air or water. The fundamental problem is that a deep space rocket would have to start out with all the propellant it will ever need. This quickly results in the need to carry more and more propellant just to propel the propellant. The breakthrough one wishes for in deep space travel is to overcome the need to carry propellant at all. How can one generate a propulsive force without carrying and ejecting propellant?
There is a force associated with the electromagnetic quantum vacuum: the Casimir force (Casimir, 1948). This force is an attraction between parallel uncharged metallic plates that has now been well measured (Lamoreaux, 1997, Mohideen, 1998, Chen et al., 2004) and can be attributed to a minute imbalance in the zero-point energy density inside the cavity between the plates versus the region outside the plates as shown in Figure 1. However, this is not useful for propulsion since it symmetrically pulls on the plates. If some asymmetric variation of the Casimir force could be identified, though, then one could in effect sail through space as if propelled by a kind of quantum fluctuation wind. Unfortunately, at this point this is pure speculation since it requires an invention to contrive such a means.
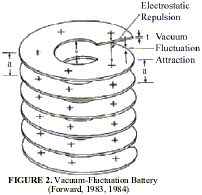
The other requirement for space travel is energy. It is sometimes assumed that attempting to extract energy from the vacuum zero-point field (ZPF) would somehow violate the laws of thermodynamics. Fortunately, it turns out that this is not the case. A thought experiment published by Forward (1983, 1984) demonstrated how the Casimir force could in principle be used to extract energy from the vacuum ZPF. He showed that any pair of conducting plates at close distance experiences an attractive Casimir force that is due to the electromagnetic ZPF of the vacuum. A vacuum-fluctuation battery can be constructed by using the Casimir force to do work on a stack of charged conducting plates (see Figure 2). By applying a charge of the same polarity to each conducting plate, a repulsive electrostatic force will be produced that opposes the Casimir force. If the applied electrostatic force is adjusted to be always slightly less than the Casimir force, the plates will move toward each other and the Casimir force will add energy to the electric field between the plates. The battery can be recharged by making the electrical force slightly stronger than the Casimir force to re-expand the foliated conductor.
Cole and Puthoff (1993) verified that (generic) energy extraction schemes are not contradictory to the laws of thermodynamics. For thermodynamically reversible processes, no heat will flow at temperature T = 0. However, for thermodynamically irreversible processes, heat can be produced and made to flow, either at T = 0 or at any other T > 0 situation, such as by taking a system out of mechanical equilibrium. Moreover, work can be done by or done on physical systems, either at T = 0 or T > 0 situations, whether for a reversible or irreversible process. However, if one is considering a net cyclical process on the basis of, say, the Casimir Effect, then energy would not be able to be continually extracted without a violation of the second law of thermodynamics. Thus, Forwards process cannot be cycled to yield a continuous extraction of energy. Here, the recharging of the battery would, owing to frictional and other losses, require more energy than is gained from the ZPF. There is no useful engine cycle in this process; nonetheless, the plate-contraction phase of the cycle does demonstrate the ability to cause extraction of energy from the ZPF. It does reflect work done by the ZPF on matter.
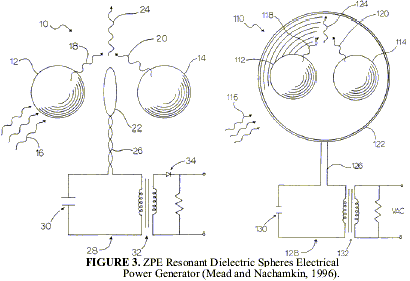
Another illustrative example of a scheme for extracting energy from the ZPF is a patent by Mead and Nachamkin (1996). They propose that a set of resonant dielectric spheres be used to extract energy from the ZPF and convert it into electrical power. They consider the use of resonant dielectric spheres, slightly detuned from each other, to provide a beat-frequency downshift of the more energetic high-frequency components of the ZPF to a more easily captured form (see two embodiments of the invention in Figure 3). Their device includes a pair of dielectric structures (items 12, 14, 112, 114 in Fig. 3) that are positioned proximal to each other and which intercept incident ZPE radiation (items 16, 116 in Fig. 3). The volumetric sizes of the structures are selected so that they resonate at a particular frequency of the incident radiation. But the volumetric sizes of the structures are chosen to be slightly different so that the secondary radiation emitted from them (items 18, 20, 24, 118, 120, 124 in Fig. 3) at resonance interferes with each other, thus producing a beat frequency radiation that is at a much lower frequency than that of the incident radiation, and that can be converted into electrical energy. A conventional metallic antenna (loop or dipole type, or a RF cavity structure; items 22, 122 in Fig. 3) can then be used to collect the beat frequency radiation. This radiation is next transmitted from the antenna to a converter via an electrical conductor or waveguide (items 26, 126 in Fig. 3) and converted to electrical energy. The converter must include: 1) a tuning circuit or comparable device so that it can effectively receive the beat frequency radiation, 2) a transformer to convert the energy to electrical current having a desired voltage, and 3) a rectifier to convert the energy to electrical current having a desired waveform (items 28, 30, 32, 34, 128, 130, 132 in Fig. 3).
The receiving structures are composed of dielectric material in order to diffract and scatter the incident ZPE radiation. The volumetric sizing requirements for the receiving structures are selected to enable them to resonate at a high frequency of the incident ZPE radiation based on the parameters of frequency (of the incident ZPE radiation) and propagation characteristics of the medium (vacuum or otherwise) and of the receiving structures. Since the ZPE radiation energy density increases with increasing frequency, greater amounts of electromagnetic energy are potentially available at higher frequencies. Consequently, the size of the receiving structures must be miniaturized in order to produce greater amounts of energy from a system located within a space or area of a given size.
Therefore, the smaller the size of the receiving structures, the greater the amount of energy that can be produced by the system. No experimental study has been performed to validate this invention and characterize its performance, or otherwise confirm or refute its claimed efficacy.
Although novel ZPF energy extraction mechanisms have been proposed in the literature (some credible, many not credible), no practicable technique has been successfully demonstrated in the laboratory. Therefore, our mission is to work with the theoretical physicists who developed the comprehensive understanding of ZPF theory along with experienced electrodynamic and RF engineers so that we can further characterize the physics of the ZPF and identify possible energy extraction techniques and test their feasibility for application to space power systems. In particular, we are pursuing experimental designs that are capable of either confirming or refuting the theoretical predictions and expectations by many experimentalists that cyclic energy can be obtained from the ZPF. Our proposed research program is to: 1) develop a theoretical framework for analyzing and developing the potential ZPF energy and extend original research as needed; 2) design and assess potential methods and techniques utilizing ZPF energy as a practical power source; 3) prepare detailed test plans for candidate experiments; 4) design and fabricate ZPF energy extraction device(s) for performance characterization and validation; 5) test the devices under appropriate space conditions, as necessary; 6) evaluate test results for application to space power and propulsion; and 7) identify necessary additional development for qualification of ZPF energy devices. In what follows, we summarize the physics of the ZPF and the experimental investigation we propose to conduct in support of our program.
# ORIGIN OF ZERO-POINT FIELD ENERGY
In the traditional quantum theory presented in many textbooks, the basis of the ZPF is attributed to the so-called Heisenberg Uncertainty Principle. According to this principle, A and B are any two conjugate observables that we are interested in measuring in a lab experiment and they must obey the commutation relation [A,B] = ih(h is Plancks reduced constant). Their corresponding uncertainty relation isDeltaA DeltaB > h/2, where DeltaA is the variance (a.k.a. uncertainty) of observable A and DeltaB is that of the conjugate observable B. This relation states that if one measures observable A with very high precision (i.e., its uncertainty DeltaA is very small), then a simultaneous measurement of observable B will be less precise (i.e., its uncertainty DeltaB is very large), and vice versa. In other words, it is not possible to simultaneously measure two conjugate observable quantities with infinite precision. This minimum uncertainty is not due to any correctable flaws in measurement, but rather reflects the intrinsic fuzziness in the quantum nature of energy and matter. Substantial theoretical and experimental work has shown that in many quantum systems the limits to measurement precision is imposed by the quantum vacuum zero-point fluctuations (ZPF) embodied within the uncertainty principle. Nowadays we rather see the Heisenberg Uncertainty Principle as a necessary consequence, and therefore, a derived result of the wave nature of quantum phenomena. The uncertainties are just a consequence of the Fourier nature of conjugate pairs of quantities (observables). For example, the two Fourier-wave-conjugates time and frequency become the pair of quantum-particle conjugates time and energy and the two Fourier-wave-conjugates displacement and wavenumber become the pair of quantum-particle conjugates position and momentum. For more on this see, e.g., Peres (1993).
Radio and microwaves, infrared light, visible light, ultraviolet light, X-rays, and gamma rays are all forms of electromagnetic radiation. Classically, electromagnetic radiation can be pictured as waves flowing through space at the speed of light. The waves are not waves of anything substantive, but are in fact ripples in the state of a field.
These waves carry energy, and each wave has a specific direction, frequency and polarization state. This is called a propagating mode of the electromagnetic field. A useful tool for modeling the (propagating mode of the) electromagnetic field in quantum mechanics is the ideal quantum mechanical harmonic oscillator: a hypothetical mass on a perfect spring oscillating back and forth under the action of the springs restoring force, which is small enough to be subject to quantum laws. The Heisenberg Uncertainty Principle dictates that a quantized harmonic oscillator (a.k.a. a photon state) can never come entirely to rest, since that would be a state of exactly zero energy, which is forbidden. Every mode of the field must have hw/2 (w is the mode/photon frequency, hw is the energy of a single mode/photon) as its average minimum energy in the vacuum. (This is a tiny amount of energy, but the number of modes is enormous, and indeed increases as the square of the frequency. The product of this tiny energy per mode times the huge spatial density of modes yields a very high theoretical energy density per unit volume.) It is for this reason that a ZPE term is added to the classical blackbody spectral radiation energy density p(w)dw(i.e., the energy per unit volume of radiation in the frequency interval [ w,w+ dw]) for when the absolute temperature T of the oscillator system becomes 0 K in the vacuum (Milonni, 1994):
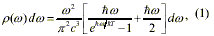
where c is the speed of light, and k is Boltzmanns constant (note: w = 2 Pi v). The factor outside the square brackets is the density of (mode/photon) states (i.e., the number of states per unit frequency interval), the first term inside the square brackets is the standard Planck blackbody radiation energy per mode, and the second term inside the square brackets is the quantum zero-point energy per mode. Equation (1) is called the Zero-Point Planck (ZPP) spectral radiation energy density.
From this line of reasoning, quantum physics predicts that all of space must be filled with electromagnetic zeropoint fluctuations (a.k.a. the zero-point field) creating a universal sea of zero-point energy. The density of this energy depends critically on where the frequency of the zero-point fluctuations cease. Since space itself is thought to break up into a kind of quantum foam at a tiny distance scale called the Planck length, lP (~ 10 -35 m), it is argued that the zero-point fluctuations must cease at the corresponding vP. If that is the case, then the zero-point energy density would be 108 orders of magnitude greater than the radiant energy at the center of the Sun. That is the extreme limit. Formally, in QED the ZPE energy density is taken as infinite. However, arguments based on quantum gravity considerations yield a finite cutoff at vP. Therefore, the spectral energy density is given byp(w)dw = ( hw3/2Pi 2c3)dw, which integrates to an energy density, u =hvP4/8Pi 2c3 ==10113 J/m3. As large as the ZPE is, interactions with it are typically cut off at lower frequencies depending on the particle coupling constants or their structure.
In SED the origin of the ZPF comes as a direct consequence of the fundamental assumptions. SED is just the ordinary classical electrodynamics of Maxwell and Lorentz where instead of taking the homogeneous solution of the source-free differential wave equations for the electromagnetic potentials, as done in traditional electrodynamics, one considers that (because there are many other moving charged particles in the distant universe) there always is the presence of a random electromagnetic background in the form of a random radiation affecting the particle(s) in our experiment. This new boundary condition replaces the null one of traditional classical electrodynamics.
Moreover, as the relativity principle dictates that identical experiments performed in different inertial frames must yield the same result, this random classical electromagnetic radiation must be the same in all inertial frames and therefore have a Lorentz-invariant energy density spectrum. But the only energy density spectrum that obeys such a condition happens to be one that is proportional to the cubic power of the frequency. Interestingly enough, this is exactly the same frequency dependence as that of the QED spectral ZPF energy density presented above when in equation (1) we set the temperature T to zero. In SED we can then write this random radiation in the same way as the ZPE of QED and we call it the classical electromagnetic ZPE. Plancks constant appears then in SED as an adjustable parameter that sets the scale of the ZPE spectral density. Several quantum results have been reproduced
In SED the origin of the ZPF comes as a direct consequence of the fundamental assumptions. SED is just the ordinary classical electrodynamics of Maxwell and Lorentz where instead of taking the homogeneous solution of the source-free differential wave equations for the electromagnetic potentials, as done in traditional electrodynamics, one considers that (because there are many other moving charged particles in the distant universe) there always is the presence of a random electromagnetic background in the form of a random radiation affecting the particle(s) in our experiment. This new boundary condition replaces the null one of traditional classical electrodynamics.
Moreover, as the relativity principle dictates that identical experiments performed in different inertial frames must yield the same result, this random classical electromagnetic radiation must be the same in all inertial frames and therefore have a Lorentz-invariant energy density spectrum. But the only energy density spectrum that obeys such a condition happens to be one that is proportional to the cubic power of the frequency. Interestingly enough, this is exactly the same frequency dependence as that of the QED spectral ZPF energy density presented above when in equation (1) we set the temperature T to zero. In SED we can then write this random radiation in the same way as the ZPE of QED and we call it the classical electromagnetic ZPE. Plancks constant appears then in SED as an adjustable parameter that sets the scale of the ZPE spectral density. Several quantum results have been reproduced by means of the classical SED approach. For a very thorough, detailed and scholarly review of SED, see de la Peña and Cetto (1996). This book was reviewed by two of us (Cole and Rueda, 1996). Nevertheless, QED and SED do not in general yield the same results for nonlinear systems, although they are in agreement for the linear systems examined. The apparent disagreements between SED and QED are quite serious, since they occur in areas that QED is highly successful. Speculatively, but quite possibly, the source of these difficulties lies in accurately dealing with the nonlinear stochastic differential equations in SED for these problems. However, even if this can be satisfied, it is most likely there will still be differences that should clearly be testable by experimental means (Cole, 2005).
# PROPOSED EXPERIMENTS
In what follows, we outline each of the proposed experimental concepts that we plan to explore theoretically and in the laboratory, though space limitations and proprietary concerns force us to limit the level of detail that we can present. The experimental and theoretical program described below has undergone preliminary evaluation by Lockheed Martin review panels involving both internal R&D personnel and outside experts on theory and experimentation.
# Voltage Fluctuations in Coils Induced by ZPF at High Frequency
In a series of experiments, Koch et al. (1980, 1981, 1982) measured voltage fluctuations in resistive wire circuits that are induced by the ZPF. The Koch et al. result is striking confirmation of the reality of the ZPF and proves that the ZPF can do real work (cause measurable currents). Although the Koch et al. experiment detected miniscule amounts of ZPF energy, it shows the principle of ZPF energy circuit effects to be valid and opens the door to consideration of means to extract useful amounts of energy.
Blanco et al. (2001) have proposed a method for enhancing the ZPF-induced voltage fluctuations in circuits. Treating a coil of wire theoretically as an antenna, they argue that the antenna-like radiation resistance of the coil should be included in the total resistance of the circuit, and they suggest that it is this total resistance that should be used in the theoretical computation of the ZPF-induced voltage fluctuations. Because of the strong dependence of the radiation resistance on the number of coil turns (scaling quadratically), coil radius (quartic scaling), and frequency (quartic scaling), these enhanced ZPF-induced voltage fluctuations should be measurable in the laboratory at quite accessible frequencies (100 MHz compared to the 100 GHz range necessary in the Koch et al. experiments).
The Blanco et al. theory is as follows. Random voltage fluctuations are conveniently described by their frequency spectrum. That is, given a time interval of measured voltages, one can Fourier transform the measurements to the frequency domain to determine how the voltage fluctuations are distributed in frequency (e.g., how much lowfrequency, long duration fluctuations are present relative to high-frequency, short-duration fluctuations).
Theoretically the spectrum of voltage fluctuations S( ,T) of a resistive circuit is given by:
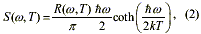
where R(w,T) is the total resistance (ohmic plus radiative), w is the (angular) frequency, and T is the absolute temperature. The resistance R(w,T) is temperature dependent through its ohmic part (the radiation resistance contribution is frequency-dependent only). The postulate of Blanco et al. is that the total resistance must include the radiation resistance of the circuit:
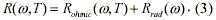
Under the assumption that the wavelengths of the ZPF modes of interest are larger than the dimensions of the circuit, the radiation resistance of a coil is given by:
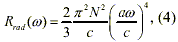
where N is the number of coil turns, and a is the radius of the coil winding.
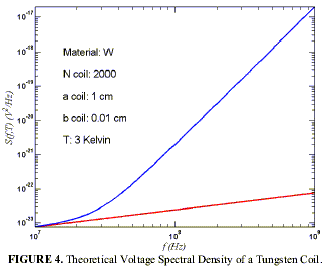
According to the Blanco et al. theory, large enhancements in ZPF-induced voltage fluctuations are possible. By reducing the temperature to minimize ohmic resistance, making the coil of many turns and large radius, and performing measurements at high frequency, it will be possible to confirm this amplification effect. Using the theory of Blanco et al., the predicted coil-enhanced voltage spectrum can be computed. For a 1 cm diameter coil of 2000 turns made of 38 AWG Tungsten wire, and at a temperature of 3 K, the result is shown in Figure 4. In Figure 4, the upper (blue) curve represents the predicted voltage spectral density for the combined ohmic plus radiation resistance. The lower (red) curve is the result when radiation resistance is ignored. If the Blanco et al. postulate is correct, the enhancement effect of the coil should be easily measured at frequencies as low as 100 MHz (where the coil enhancement effect is about 100-fold for Tungsten).
To successfully measure the ZPF-induced voltage fluctuations, the requirements of low temperature, large coil, and high frequency must be met. The low-temperature requirement is met by performing the experiment in a cooled dewar. There are laboratories with high-quality dewars (pumped down to 3 K) and sensitive instruments suitable for the measurements. The cold spot in one particular dewar under consideration is cylindrical, 2.5 cm in diameter and height. Thus the largest coil that we can consider will have a coil radius of approximately a = 1 cm. To keep the linear dimension of the coil small, we will require small wire thicknesses, say b = 0.01 cm (gauge 38 AWG). By winding the coil in a number of layers (10 or 12 layers) we can accommodate a large number of turns, say N = 2,000 turns. To minimize ohmic resistance, wire made of tungsten (W) is preferred. However, copper (Cu) is a suitable alternative providing significant cost savings.
Voltage fluctuations in the 100 MHz range are easily detected using fairly common laboratory equipment. We could perform this experiment using tungsten without resorting to the sophisticated/costly techniques used by Koch et al. to attain their extremely high frequency measurements (involving resistively shunted Josephson junctions).
For a copper wire coil, the magnitude of the enhancement effect is reduced somewhat compared to the tungsten case of Figure 4, but for frequencies approaching the GHz regime, the radiation resistance enhancement effect is still over four orders of magnitude. Equipment easily obtained will allow measurements of the voltage spectrum in the GHz regime. Therefore, given the cost tradeoff of coil fabrication for copper vs. tungsten, we may use copper coils and perform the experiment. Suitable coils will be fabricated by a custom coil-winding vendor, and a second coil will be tested. The second coil will be used in a control experiment. It will be constructed with the same parameters as the first coil, but will have half of its turns wound in the reverse direction. This will make the coil non-inductive so that its voltage spectral density should correspond to the lower red curve in Figure 4.
# ZPF Energy Extraction by Ground State Energy Reduction
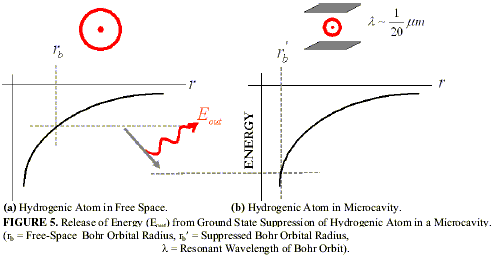
As first analyzed by Boyer (1975) and later refined by Puthoff (1987), the following paradox was addressed that even though atomic ground states involve electrons in accelerated motion, such states are nonetheless radiationless in nature. This ground state characteristic was shown to be interpretable (for the standard Bohr ground state orbit of the hydrogen atom) as an equilibrium process in which radiation by the electron in its ground state orbit was compensated by absorption of radiation from the background vacuum electromagnetic ZPE. This interpretation has recently been strengthened by the analyses of Cole and Zou (2003, 2004) using a stochastic electrodynamic (SED) model for the vacuum ZPE. Since the balance between emitted orbital-acceleration radiation and absorbed ZPE radiation is modeled as taking place primarily at the ground state orbital frequency, we can consider the possibility of using this feature in a mechanism to extract energy from the ZPE.
By passing monatomic gas atoms through specially constructed microcavities (e.g., resonant conducting Casimir cavities), which suppress the background vacuum ZPE at the ground state frequency (thereby upsetting the balance), one might expect the ground state orbit to drop in energy to a new equilibrium orbit and release the energy difference (see Figure 5). Such a process would mimic the usual radiation emission of an electron dropping from an excited state to the ground state, although in this case the excited state is the free-space ground state and the final state is the new lower-energy equilibrium ground state resulting from the effects of cavity mode suppression.
Microcavity fabrication to match the atomic ground states is daunting because there will potentially be fabrication irregularities that cause edge and surface effects which act upon the particles as they enter or exit the Casimir region. It will be a challenge to properly account for this so as to disentangle the effects from experimental results. However, further investigation showed that this principle is broadly applicable to other than just atomic ground states, e.g., to the ground state harmonic-oscillator-type vibrational motion of, say, an H2 molecule. The estimated power output under optimized conditions from this experimental approach is estimated to be on the order of Watts to kiloWatts.
An exploratory effort to investigate the above concept was carried out by Puthoff et al. (2001). In their experiment H2 gas was passed through a 1 um Casimir cavity to suppress the ZPE radiation at the vibrational ground state of the H2 molecule (see Figure 6). The anticipated signature for such a process would be increased dissociation energy of the molecule. For this purpose, the experiment was carried out at the Synchrotron Radiation Center at the University of Wisconsin at Madison, where an intense UV beam to disassociate gas molecules could be generated.
Unfortunately, problems with the synchrotron beam (unrelated to the experiment) prevented a definitive result from being obtained, so the efficacy of this ZPE-extraction approach remains undetermined at the present time. Further experimentation of this type will be explored with regard to ZPE extraction.

# Tunable Casimir Effect
The Casimir Effect is a unique ZPF-driven quantum force that occurs between closely-spaced conductive cavity walls (or plates). If left unfettered, the plates will collapse together and energy is converted from the ZPF into heat (or other forms of energy) in accordance with the expression E/A =Pi2 hc/720d3, where E/A is the energy per unit area of the plates and d is the plate separation. Further investigation of this mechanism by Cole and Puthoff (1993) showed that this process not only did not violate energy conservation, but it was compatible with thermodynamic constraints as well.
Although the Casimir force is conservative, and thus the Casimir device might appear to be a one-shot device, the fact that the attractive Casimir force is weaker for dielectric plates compared to conductive plates raises the possibility of the use of thin-film switchable mirrors to obtain a recycling engine (Puthoff, 1985, Lipkin, 1996, Pinto, 1999). In such an application the plates are drawn together by the stronger force associated with the conducting state and withdrawn after switching to the dielectric state. Under the most optimistic conditions for eventual embodiment in practical devices (where negligible energy is required for switching, oscillation between 30 nm and 15 nm spacing can be achieved for 1 cm2 plates, driving circuit +- 10 times the weight of the Casimir plates, etc.), an estimate based on a switching oscillation from a purely conductive state to a dielectric constant of K = 4 yields a figure of merit of +- 35 x f(MHz) W/kg (f = switching rate) for the power density (Puthoff, 1985). This can be compared to the power density of +- 5 W/kg achieved by radioisotope thermoelectric generators. The predicted output power per unit area for this experimental device is +- 10 -6 f(MHz)/4[d( um)]3 Watts/cm2.
Another tunable conductive-type plate experiment under consideration involves the use of plates consisting of three-dimensional photonic crystals with the bandgap of the photons that can transmit through the structure being a Another tunable conductive-type plate experiment under consideration involves the use of plates consisting of three-dimensional photonic crystals with the bandgap of the photons that can transmit through the structure being a tunable value. Using microelectromechanical processing methods, Sandia National Laboratories has experimentally produced such crystals and are researching methods of actively modifying the structures while in use (Lin et al., 2003). Finally, the technology requirements for this experimental concept are the nano-fabrication of microcavities with thin-film deposited surfaces, RF-driven piezoelectric mounts for cavity oscillation, mirrorswitching modality (e.g., hydrogen pressure modulation), and calorimetric measurement of energy/heat production.
# Electron Inertial Mass Test
Another interesting concept to explore is a postulated electron mass change caused by the exclusion of ZPF modes between Casimir plates, which would result in a change in the optical path-length of a laser beam passing through the cavity compared to a beam not passing through it. According to the quantum vacuum inertia hypothesis (Haisch et al., 1994, 2001, Rueda and Haisch, 1998a, 1998b, 2005), as well as the connectivity approach of Nickisch and Mollere (2002), at least some component of inertial mass derives from charge interactions with the ZPF. It is possible to investigate the electromagnetic basis of inertial mass experimentally by using Casimir plates immersed in a plasma. The Casimir plates are enclosed in a vacuum tube in which uniformly distributed plasma is created. A laser beam is split three ways, as shown in Figure 7. One laser beam is directed between the Casimir plates, and the other two outside the plates. The goal is to combine Beams 1 and 2, and, separately, Beams 2 and 3 and to look for interference fringe shifting of the 2-3 combination relative to the 1-2 combination. Under the postulated effect this fringe shift would be due to an inertial mass change of the electrons between the plates. Note that the electron plasma frequency fplasma is given (in Gaussian units) by:
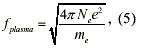
where Ne is the electron number density, e is the electron charge, and me is the electron mass. The index of refraction of the plasma is given by:
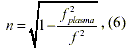
where f is the frequency of the laser. Any electron mass change caused by the exclusion of ZPF modes between the Casimir plates would result in a change in the optical path-length for Beam 3 and produce a corresponding interference fringe shift. It might be possible to attach the plates to a device for changing the plate separation and look for interference fringe shifting as a function of plate separation. Alternatively, a Casimir tube could be used instead of plates for enhanced effect since the Casimir ZPF exclusion would then occur in two dimensions instead of only one. We will be investigating the feasibility of this experiment, including working out the best combination of laser frequency and plasma density and calculating the magnitude of the effect expected.
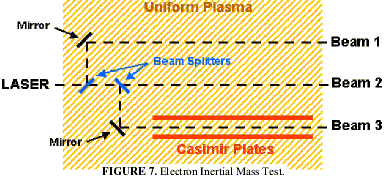
# CAVEAT EMPTOR!
There has been a large amount of popular semi-technical literature published over the last 25 years covering the topic of extracting energy from the quantum vacuum field. The literature is mostly composed of self-published books or pamphlets found in bookstores or on the internet, and there are also professional society conference papers that are largely not peer-reviewed. Unfortunately, much of this literature is published within the context of free energy and antigravity devices with claims that the vacuum ZPE is the source that drives free energy devices or powers an antigravity craft, or powers gravity/mass modification or repulsive gravitational force beam devices, etc.
A number of these claims have been evaluated over the years by credentialed scientists and were falsified. Much of this literature is self-serving marketing propaganda, and the language describing the physics or engineering principles for these claims is often couched in what we call technobabble. Credentialed scientists interested in seriously pursuing a laboratory investigation of the vacuum ZPF should be forewarned that many of the claims being made in the non-peer-reviewed literature are fraught with pathological science, fraud, misinformation, disinformation, and spurious physics. This is the reason why the present authors were very selective about which ZPE extraction approaches to consider for our research program.
# CONCLUSION
We reviewed the physical nature of the quantum vacuum field, and described its spectral characteristics and latent energy content. We are interested in concepts that provide an experimental framework for exploring the possibility and limitations of accessing energy from the space vacuum environment. The theoretical approaches guiding this experimental investigation are based on the QED and SED models of the ZPF. The purpose of our investigation is to explore the question of whether the quantum vacuum field contains useful energy that can be exploited for space power and propulsion applications under the action of a catalyst, or cavity structure, so that energy conservation is not violated. We identified six experiments that have the potential to extract useful energy from the vacuum. One of these, Forwards Vacuum-Fluctuation Battery, was shown to be unsuitable for completing an engine cycle for pumping energy from the vacuum. The efficacy of the Mead and Nachamkin patent device has not yet been evaluated in the lab. However, four additional experimental concepts are potentially exploitable and we have selected those to pursue in a carefully guided theoretical and laboratory research program. The estimated power output from three of these concepts could under optimum conditions range from Watts to kiloWatts. But it should be stressed that there potentially is a real theoretical and experimental challenge in modeling and predicting noise sources, edge and surface effects, etc. within the different experimental approaches, so that experimental results are unambiguously interpretable. If successful, however, it is anticipated that these experiments would lead to a revolution in the way we generate electrical power for commercial and space applications.
# ACKNOWLEDGMENTS
The authors wish to thank Lockheed Martin Space Systems, the Institute for Advanced Studies at Austin, ManyOne Networks, Boston University, and California State University-Long Beach for their institutional support of this research program. We are also grateful to Jeff Newmeyer (Lockheed Martin) for very useful comments.
# REFERENCES
– Blanco, R., França, H. M., Santos, E., and Sponchiado, R. C., Radiative noise in circuits with inductance, Phys. Lett. A 282, 349-356 (2001).
– Boyer, T. H., Random electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation, Phys. Rev. D 11, 790-808 (1975).
– Casimir, H. B. G., On the Attraction Between Two Perfectly Conducting Plates, Proc. Kon. Ned. Akad. Wetensch. 51, 793-796 (1948).
– Chen, F., et al., Theory confronts experiment in the Casimir force measurements: Quantification of errors and precision, Phys. Rev. A 69, 022117 (2004).
– Cole, D. C., Simulation Results Related to Stochastic Electrodynamics, in proc. of the intl conf. Quantum Theory: Reconsideration of Foundations-3, AIP Press, 2005, in press.
– Cole, D. C., and Puthoff, H. E., Extracting energy and heat from the vacuum, Phys. Rev. E 48, 1562-1565 (1993).
– Cole, D. C., and Rueda, A., The Quantum Dice: An Introduction to Stochastic Electrodynamics, Found. Phys. 26, 1559-1562 (1996).
– Cole, D. C., and Zou, Y., Quantum Mechanical Ground State of Hydrogen Obtained from Classical Electrodynamics, Phys. Lett. A 317, 14-20 (2003).
– Cole, D. C., and Zou, Y., Analysis of Orbital Decay Time for the Classical Hydrogen Atom Interacting with Circularly Polarized Electromagnetic Radiation, Phys. Rev. E 69, 016601 (2004). de la Peña, L., and Cetto, A. M., The Quantum Dice: An Introduction to Stochastic Electrodynamics, Kluwer, Dordrecht, Holland, 1996.
– Forward, R. L., Alternate Propulsion Energy Sources, Final Report AFRPL TR-83-067, Air Force Rocket Propulsion Laboratory, Air Force Space Tech. Ctr. Space Div., Air Force Systems Command, Edwards AFB, CA, 1983, pp. A1-A14.
– Forward, R. L., Extracting Electrical Energy from the Vacuum by Cohesion of Charged Foliated Conductors, Phys. Rev. B 30, 1700-1702 (1984).
– Haisch, B., Rueda, A., and Dobyns, Y., Inertial mass and the quantum vacuum fields, Ann. der Phys. 10, 393-414 (2001).
– Haisch, B., Rueda, A., and Puthoff, H. E., Inertia as a zero-point-field Lorentz force, Phys. Rev. A 49, 678-694 (1994).
– Koch, R. H., Van Harlingen, D. J., and Clarke, J., Quantum-Noise Theory for the Resistively Shunted Josephson Junction, Phys. Rev. Lett. 45, 2132-2135 (1980).
– Koch, R. H., Van Harlingen, D. J., and Clarke, J., Observation of Zero-Point Fluctuations in a Resistively Shunted Josephson Tunnel Junction, Phys. Rev. Lett. 47, 1216-1219 (1981).
– Koch, R. H., Van Harlingen, D. J., and Clarke, J., Measurements of quantum noise in resistively shunted Josephson junctions, Phys. Rev. B 26, 74-87 (1982).
– Lamoreaux, S. K., Demonstration of the Casimir Force in the 0.6 to 6m Range, Phys. Rev. Lett. 78, 5-8 (1997).
– Lin, S. Y., Moreno, J., and Fleming, J. G., Three-dimensional photonic-crystal emitter for thermal photovoltaic power generation, Appl. Phys. Lett. 83, 380-382 (2003).
– Lipkin, R., Thin-film mirror changes into a window, Science News 149, 182 (1996).
– Mead, F. B., and Nachamkin, J., System for Converting Electromagnetic Radiation Energy to Electrical Energy, United States Patent No. 5,590,031 (1996).
– Milonni, P. W., The Quantum Vacuum: An Introduction to Quantum Electrodynamics, Academic Press, New York, 1994, pp. 1- 33, 290-294.
– Mohideen, U., Precision Measurement of the Casimir Force from 0.1 to 0.9m, Phys. Rev. Lett. 81, 4549-4552 (1998).
– Nickisch, L. J., and Mollere, J., Connectivity and the Origin of Inertia, arxiv.org/PS_cache/physics/pdf/0205/0205086.pdf (2002).
– Peres, A., Quantum Theory: Concepts and Methods, Kluwer, Dordrecht, Holland, 1993.
– Pinto, F., Engine cycle of an optically controlled vacuum energy transducer, Phys. Rev. B 60, 14740-14755 (1999).
– Puthoff, H. E., Vacuum energy extraction by conductivity switching of Casimir force, Technical Memo, Inst. for Advanced Studies at Austin, 1985.
– Puthoff, H. E., Ground state of hydrogen as a zero-point-fluctuation-determined state, Phys. Rev. D 35, 3266-3269 (1987).
– Puthoff, H. E., Little, S. R., and Ibison, M., Discussion of experiment involving lowering of ground state energy for oscillation in a Casimir cavity, Intl Conf. on Squeezed States and Uncertainty Relations (ICSSUR 2001): Special Session on Topics of Physics Related to Stochastic Electrodynamics, Boston University, 2001.
– Rueda, A., and Haisch, B., Inertia as reaction of the vacuum to accelerated motion, Phys. Lett. A 240, 115-126 (1998a).
– Rueda, A., and Haisch, B., Contribution to inertial mass by reaction of the vacuum to accelerated motion, Found. Phys. 28, 1057-1108 (1998b).
– Rueda, A., and Haisch, B., Gravity and the quantum vacuum inertia hypothesis, Ann. der Phys. 14, 479-498 (2005).