##Znidarsic, Franck P.E, PART 2:
# Online preview of historic of “Zero Point Technologies” : (Open the original pages links to see the numerous pictures and videos)
# CHAPTER FOUR, THE ZERO POINT INTERACTION : http://www.angelfire.com/scifi2/zpt/chapter4.html
(see picture on original webpage) This author conducts a cryogenic zero point energy experiment. The results were published by Hal Fox in “New Energy News vol 5 pg #19.
# HISTORY AND DISCOVERY
In the mid 1970s Ray Frank (the owner and president of the Apparatus Engineering Company one of my former employers) assigned this author the task of building a ground monitoring relay. In an effort to complete this assignment, I began to experiment with coils, current transformers, and magnetic amplifiers. I succeeded in developing the device. We sold many hundreds of them to many mining companies. I applied the knowledge that I gained to the design of an electronic levitational device. To my dismay, I discovered that no combination of electrical coils would induce a gravitational field.
In the mid 1980’s, a friend, Tom C. Frank, gave me the book, ” THE QUEST FOR ABSOLUTE ZERO” by Kurt Mendelssohn. In his book, Mendelssohn disclosed that the relationship between the forces changed at cryogenic temperatures. This was the clue that I needed. Things began to come together. In 1989, I wrote my first book on the subject, “Elementary Antigravity” . This book caught the eye of Ronald Madison , a far sighted manager at the Pennsylvania Electric Company (my past employer). In 1991, Ron persuaded me to go to Texas and visit with Dr. Harold Puthoff . Puthoff’s work is based on the ideas of Andrei Sakharov. My work is based of the work of Kurt Mendelssohn. It is truly astounding that Puthoff and I, each following separate paths, independently arrived at almost the same conclusions.
Prior to meeting Puthoff, I knew that the relationship between the forces changed in condensed cryogenic systems. Puthoff explained that the phenomena that I had discovered was the zero point interaction. Zero point interactions have now been discovered other non-cryogenic condensed systems. Zero point phenomena are exhibited in cold fusion cells and in the gravitomagnetic effects produced by rotating superconductors.
# IN THE BEGINNING
In 1989 this author came out with his first book “Elementary Antigravity”. In chapter 10 of this book the relationship between the forces within cryogenic systems was examined. In 1996 an intermediate version of this material was published in the “Journal of New Energy” Vol 1, No 2. The remainder of this chapter is essentially a rewrite of these two works. As then, the study of cryogenic phenomena is very instructive. A better understanding of all zero point technologies can be gained through the study of cryogenic phenomena.
” Zero point energy is the energy that remains after a substance is cooled to absolute zero. ” Dr. Hal Puthoff
# INTRODUCTION
It is well known that superconductors offer no resistance to electrical currents. Less well known, but even more amazing, are the low temperature superfluids. These fluids flow without friction. Once set into motion, they never slow down. Quantum interactions are limited to atomic distances in normal substances. In superconductors and superfluids quantum interactions are observed on a macroscopic scale. The normal interaction of the magnetic and electric field is very different in a superconductor. In normal conductors changing fields are required to induce other fields. In superconductors static fields can also induce other fields.1At the root of these effects lies a dramatic change in the permittivity and permeability of a superconductor (electron condensation). Ordinarily this change only effects the electromagnetic field. This author has developed techniques to coerce the gravitational and nuclear forces to participate in the condensation. A new look at the electromagnetic effects will lead to a deeper understanding of the the zero point interaction.
# THE ELECTRIC FIELD
The electric field of an isolated electric charge is that of a monopole. Dr. George Mathous, instructor at the Indiana University at Pennsylvania, commonly described the electric field of an isolated charge by stating, “The field drops off with the square of the distance and does not saturate.” In lay words this means that the field diverges outward and extends to infinity.
# THE FIELD OF AN ISOLATED ELECTRIC CHARGE
It is instructive to look at the range and the strength of the electric field. The range of the field associated with an isolated electric charge is infinite. Isolation requires resistance. The electrical resistance of a superconductor is zero. No isolated charges can exist within a superconductor. The infinite permittivity of a superconductor confines the electric field within the superconductor. No leakage flux escapes. The maximum range of the electric field equals the length of the superconductor.
# THE MAGNETIC FIELD
Mangetic flux lines surround atoms and nucleons. The length of the shortest of these flux lines is measured in Fermi meters. The magnetic permeability of a superconductor is zero. All magnetic flux lines are expelled. This phenomena is known as the Meissner effect. The minimum range of the magnetic field equals the circumference of the superconductor.
# THE QUANTUM FORCES
The infinite permittivity and permeability of superconductors also effects the quantum forces. The quantum forces normally have a very short range of interaction. This range is confined to atomic dimensions. Quantum interactions are observed on a macroscopic scale in superconductors and superfluids. Superconductors only accept currents that are integer multiples of one another. Superfluid helium will spin in a small cup only at certain rotational speeds. These low temperature phenomena vividly demonstrate that the range of the quantum interaction has increased to macroscopic dimensions.
http://www.angelfire.com/scifi2/zpt/sounds/constant.wav Pick the link to hear a quote from the lecture at the University of Illinois. File type wave. September 1999 )
http://www.angelfire.com/scifi2/zpt/images/zpe.gif A main point. Pick to view a chart that shows how the range of force interaction changes in a vibrationally reinforced condensate. )
Moses Chan and Eun-Seong Kim cooled and compressed helium and discovered a new phase of matter. They produced the first supersolid. 8The results surprised the physics community. Parts of the solid mass passed through other parts of the solid mass without friction. Friction is produced by the interaction of the electrical forces that bind solids together. These electrical forces are known as Columbic potentials. The individual Columbic potentials of normal matter become smoothed out in a supersolid. The electrical forces act in unity to produce a smooth frictionless surface. Nuclear fusion is regulated by the Columbic potential of the nucleus. The Columbic potential of the nucleus is also smoothed out in certain Bose condensates. Nuclear fusion can progress by unusual routes in these condensates.
# THE NUCLEAR FORCES
This author attended the American Nuclear Society’s Low Level Nuclear Reaction Conference in June of 1997. The conference was held at the Marriot World Trade Center in Orlando. At that conference James Patterson presented his new composite beads. These beads reduce the radioactivity of nuclear waste. George Miley described his discovery of heavy element transmutations within the CETI beads. The discovery of heavy element transmutations has given the field a new name. It is no longer called “cold fusion.” The process is now called ” low level nuclear transmutation “.
The nucleus is surrounded by a strong positive charge. This charge strongly repels other nucleons. Conventional wisdom has it that the only way to get two nucleons to fuse together is to overcome this repulsive effect. In hot fusion scientists have been attempting (for 50 years now) to fuse nucleons together by hurtling them at each other a high speed. The nucleons must obtain at least ten thousand electron volts of velocity to overcome the electrostatic barrier. The process of surmounting the repulsive electrostatic barrier is akin to traveling swiftly over a huge speed bump. In the case of the speed bump, a loud crash will be produced. In the case of the electrostatic barrier, gamma and X-rays are produced. In conventional hot fusion huge quantities radiation are given off by this process. If the Patterson cell worked by this conventional process, everyone near it would have been killed.
… During the conference in Orlando, Professor Heirich Hora (left), Emeritus Professor of The University of New South Wales, presented his theory of how the electrostatic barrier was being overcome. Hora said that the repulsive positive charges of the nucleons were “screened” by a negatively charged electron cloud. 2
Dr. Hora’s theory can not explain the lack of radiation. In his model the nucleons must still pass over the electrostatic potential barrier. When they do a high energy signatures will be produced.
If the range of the strong nuclear force increased beyond the electrostatic potential barrier a nucleon would feel the nuclear force before it was repelled by the electrostatic force. Under this situation nucleons would pass under the electrostatic barrier without producing any radiation. Could this author’s original idea that electron condensations increase the range of the nuclear foces be correct?
Since the Orlando conference several two new things have come to light.
– 1. It is now known that John J. Ruvalds discovered high temperature thin film nickel hydrogen superconductors.
Light water cold fusion cells (the CETI cell) are thin film nickel hydrogen structures.
Patent nuber 4, 043, 809 states: ” High temperature superconductors and method
ABSTRACT: This invention comprises a superconductive compound having the formula: Ni1-x Mx Zy wherein M is a metal which will destroy the magnetic character of nickel (preferably copper, silver or gold); Z is hydrogen or deuterium, x is 0.1 to 0.9; and y, correspondingly, 0.9 to 0.1, and method of conducting electric current with no resistance at relatively high temperature of T>1° K comprising a conductor consisting essentially of the superconducting compound noted above.”
This patent was issued on August 23, 1977 long before cold fusion was discovered. The bulk of the nickel hydrogen material becomes superconductive at cryogenic temperatures, however, this author believes that small isolated areas of superconductivity exist within the material at room temperature.
– 2. F. Celani, A. Spallone, P. Tripodi, D. Di Gioacchino, S. Pace, INFN Laboratori Nazionali di Frascati, via E.Fermi 40, 00044 Frascati (Italy) discovered superconductivity in palladium deuterium systems.
” OBSERVATIONS OF STRONG RESISTIVITY REDUCTION IN A PALLADIUM THIN LONG WIRE USING ULTRA-HIGH FREQUENCY PULSED ELECTROLYSIS
“…………Awire segment (1/4 of total, the most cathodic) showed a very low resistance behavior in some tests (corresponding to R/Ro values much less than 0.05 and in a case less than 0.01)………………”
It appears that the palladium deuterium structure is a room temperature superconductor. Heavy water cold fusion cells are constructed of palladium impregnated with deuterium (deuterium is heavy hydrogen).
– 3. Superconductors have no need to be negative, New Scientist, issue 2498, May 2005
” Now physicist Julian Brown of the University of Oxford is arguing that protons can also form pairs and sneak through the metallic lattice in a similar manner. In theory, the protons should superconduct, he says. ”
It’s now known that cold fusion cells contain small superconductive regions.34 Nuclear reactions proceed in these regions after thermal energy is added to the system. The thermal vibrations invite protons to participate in the condensation. The permeability and the permittivity of condensation now affects the nuclear forces. This author contends that the range of the strong nuclear force extends beyond the range of the electrostatic potential barrier. The increase in range allows nuclear transmutations to take place without radiation.
# SONOFUSION
The Griggs Machine and Potapov’s Yusmar device have been claimed to produce anomalous energy. The conditions inside of a cavitational bubble are extreme and can reach 10 of thousands degrees C at pressures of 100 million atmospheres or more.5These horrific pressures and temperatures are still several orders a magnitude to small to drive a conventional hot fusion reaction.
In January of 1998 P. Mohanty and S.V. Khare, of Maryland College, reported: Sonoluminesence as a Cooperative Many Body Phenomenon , Physical Review Letters Vol 80 #1 January 1998.
“……..The long range phase correlation encompassing a large number of component atoms results in the formation of a macroscopic quantum coherence……”
A superconductor is a macroscopic quantum coherence. This author believes that the condensed plasma within a cavitation bubble is superconductive. Cavitational implosions produce extreme shock . This shock invites the nuclear force to participate in the condensation. The range of the nuclear force is increased. Nuclear transmutations proceed within the condensation.
# GRAVITY
It was believed, during the first half of the 20th Century, that antigravity would be discovered shortly. This never happened. By the second half of the 20th Century, mainstream scientists believed that the that the unification of gravity and electromagnetism could only be obtained at very high energies. These energies would forever be beyond the reach of man’s largest accelerators. Antigravity was relegated to the dreams of cranks.
In 1955 Major Donald E. Keyhole wrote in the “The Flying Saucer Conspiracy” Page 252-254
“Even after Einstein’s announcement that electricity, magnetism, and gravity were all manifestations of one force, few people had fully accepted that thought that we might someday neutralize gravity. … I still had no idea how such a G-field could be created.”
In the last decade of the 20th Century, Podkletnov applied mechanical shock to a superconductor. A gravitational anomaly was produced.6Znidarsic wrote that the vibrational stimulation of a Bose condensate adjoins the gravitational field with the condensate. The gravitational force is then effected by the permittivity and permeability of the condensate. The range of the gravitational interaction decreases by the same order of magnitude that the range of the nuclear force has increased. The strength of the gravitational field within the condensate greatly increases. Gravitomagnetic flux lines are expelled. This takes place at low energies. It has to do with the path of the quantum transition. The relationship will be qualified in later chapters. Hopefully this idea will someday be universally recognized and antigravity will finally become a reality.
# RELATED DEVELOPMENT
On July 12, 1998 the University of Buffalo announced its discovery: CARBON COMPOSITES SUPERCONDUCT AT ROOM TEMPERATURE
SUPERCONDUCTION AT ROOM TEMPERATURE: NEGATIVE ELECTRICAL RESISTANCE SEEN IN CARBON COMPOSITES
“LAS VEGAS — Materials engineers at the University at Buffalo have made two discoveries that have enabled carbon-fiber materials to superconduct at room temperature.
The related discoveries were so unexpected that the researchers at first thought that they were mistaken.
Led by Deborah D.L. Chung, Ph.D., UB professor of mechanical and aerospace engineering, the engineers observed negative electrical resistance in carbon-composite materials, and zero resistance when these materials were combined with others that are conventional, positive resistors…..
This finding of negative resistance flies in the face of a fundamental law of physics: Opposites attract.Chung explained that in conventional systems, the application of voltage causes electrons — which carry a negative charge — to move toward the high, or positive end, of the voltage gradient.
But in this case, the electrons move the other way, from the plus end of the voltage gradient to the minus end………………..”In this case, opposites appear not to attract,” said Chung. The researchers are studying how this effect could be possible.”…………………..A patent application has been filed on the invention. Previous patents filed by other researchers on negative resistance have been limited to very narrow ranges of the voltage gradient.
In contrast, the UB researchers have exhibited negative resistance that does not vary throughout the entire gamut of the voltage gradient.”7
Electrical engineers know that when electrons “move toward the high, or positive end, of the voltage gradient” power is produced. Have the University of Buffalo scientists discovered how to produce electricity directly from a zero point process?
# CONCLUSION
The range of the electric and magnetic fields are strongly effected by a superconducting Bose condensate. An element of shock invites nuclear and gravitational participation. The shock produces vibration . The vibration lowers the elasticity of the space within the condensate. The reduced stiffness is expressed in several ways. The range of the natural forces tend towards the length of the superconductor. The strength of the forces varies inversly with their range. The constants of the motion tend toward the electromagnetic. The effect of the vibration is qualified in Chapters 10 and 11.
The development or reduced to practice zero point technologies will be of great economic and social importance.
# NOTES :
1. K. Mendelssohn. ” THE QUEST FOR ABSOLUTE ZERO ” McGraw-Hill, New York, 1966
2. Hora, Kelly Patel, Prelas, Miley, and Tompkims; Physics Letters A, 1993, 138-143 Screening in cold fusion derived from D-D reactions
Dr. George Miley’s “Swimming Electron Theory” is based on the idea that electron clusters (a form of condensation) exist between the metallic surfaces of cold fusion electrodes.
3. Cryogenic phenomena are commonly associated with the spin pairing of electrons. The Chubb – Chubb theory points out the fact that electrons pair in the cold fusion process.
4. A. G. Lipson, et al., ” Generation of the Products of DD Nuclear Fusion in High-Temperature Superconductors YBa2Cu3O7-x Near the Superconducting Phase Transition,” Tech. Phys., 40 (no. 8), 839 (August 1995).
5. “Can Sound Drive Fusion in a Bubble” Robert Pool, Science vol 266, 16 Dec 1994
6. “A Possibility of Gravitational Force Shielding by Bulk YBa2Cu3O7- x Superconductor” , E. Podkletnov and R. Nieman Physica C 203 (1992) pp 441-444.
“Tampere University Technology report” MSU-95 chem, January 1995
“Gravitoelectric-Electric Coupling via Superconductivity. ” Torr, Douglas G. and Li, Ning Foundations of physics letters. AUG 01 1993 Vol6 # 4, Page 371
7. Companies that are interested in technical information on the invention should contact the UB Office of Technology Transfer at 716-645-3811 or by e-mail at lohrman@research.buffalo.edu.
“Apparent negative electrical resistance in carbon fiber composites”, Shoukai Wang, D.D.L. Chung ; The Journal “Composites”, September 1999 http://www.composites.ubc.ca/CompositesOnline/Articles.asp
8. “Probing Question: What is a supersolid?” PhysicsOrg.com, May 13, 2005
// End of chapter 4 …………………………………………………………………..
# CHAPTER #5, GENESIS. A version of this chapter was published in “Infinite Energy” Vol 1, #5 & #6 1996. http://www.angelfire.com/scifi2/zpt/chapter5.html
NOTES
– 1 – Edward P. Tryon, NATURE VOL 246, December 14, 1973.
– 2 – Technically, nothing can exist outside of the universe. The universe is a closed structure in which, according to the cosmological principle, all positions are equivalent. The model presented in this paper, in which an object falls from an infinite distance away to the edge of the universe, does not represent reality. The model does, however, allow for the calculation of the negative gravitational potential shared by all objects within the universe.
– 3 – “…the Universe is, in fact, spherical…” Lisa Melton, SCIENTIFIC AMERICAN, July 2000, page 15
– 4 – Fritz Zwicky proposed that 90% of the matter in the universe is “dark” in 1933. He came to this conclusion from the study of clusters of galaxies.
Vera Rubin confirmed that 90% of the universe’s matter is composed of the so called “dark matter” from her study of the rotational speeds of galaxies in 1977.
Solgaila and Taytler found that the universe contains 1/4 proton of ordinary matter and 8 protons of dark matter per cubic meter. ” New Measurements of Ancient Deuterium Boost the Baryon Density of the Universe “, Physics Today, August 1996, Page 17
– 5 – A satellite gyroscope experiment actually measured the gravitomagnetic field. Schwinger “Einstein’s Legacy” Page 218, The Scientific American Library.
– 6 – “Inertial is a much-discussed topic. The Graneaus give a beautiful account in which they relate theories of inertia back to those of Mach at the beginning of the century. They view inertia as the result of the gravitational interaction of all particles in the universe on the body in question…”
Professor John O’ M. Bockris Journal of Scientific Exploration, Spring 1995
– 7 – The genesis process may currently be creating particles in inter-steller space. “Energy from Particle Creation in Space” Cold Fusion (12/94) No. 5, page 12; Wolff, Milo 6. Paul Davies and John Gribbin, “THE MATTER MYTH” Touchstone publishing 1992.
– 8 – Hal Puthoff, PHYSICAL REVIEW A, March 1989 ; Hal Puthoff, D.C. Cole, PHYSICAL REVIEW E, August 1993. Hal Puthoff, OMNI, “Squeezing Energy From a Vacuum” 2/91
Puthoff manufactured very dense plasma while working with Jupiter Technologies 1990. “Compendium of Condensed-Charge Technology Documentation” Internal report, Jupiter Technologies 1989. A patent on the process was obtained by Ken Shoulders #5018180.
– 9 – A ball lightning experiment in Japan appeared to produce excess energy. Y.H. Ohtsuki & H. Ofuruton, NATURE VOL 246, March 14, 1991
– 10 – Dr. McKurbe’s cold fusion experiments at SRI in the USA continue to produce unexplained excess energy. Jerry E. Bishop, The WALL STREET JOURNAL 7/14/94.
– 11 – Dr. Miley of the Hot Fusion Studies Lab at the University of Illinois developed his theory, “The Swimming Electron Theory” This theory shows that high density electron clouds exist in the CETI cold fusion cell.
– 12 – Andrei Sakharov SOVIET PHYSICS DACKLADI Vol 12, May 1968, Page 1040
– 13 – V Arunasalam, ” Superfluid Quasi Photons in the Early Universe ” ; Physics Essays vol. 15, No. 1, 2002
– 14 – See Chapter 12 Pg 1 ” Is Radiation of Negative Energy Possible? “, F.X.. Vacanti and J. Chauveheid, Physics Essays , Vol. 15. , Number 4, 2002
Additional reading on synthetic life
– ” In the Business of Synthetic Life “, James J. Collins, Scientific American , April 2005
– ” Yikes! It’s Alive! ” , Bennett Daviss, Discover , December 1990
– In 1953 in Chicago Stanley Miller produced the first synthitic amino-acids, since then scientists have manufactured synthetic proteins.
// end of chapter 5 …………………………………………………………………..
# CHAPTER 6, NATURAL SYMMETRIES http://www.angelfire.com/scifi2/zpt/chapter6.html
INTRODUCTION
The principles upon which modern science is based can be traced back to the original notions of ancient philosophers. The greatest of these early philosophers was Aristotle (384-322 BC). Aristotle developed his ideas from within through a process of introspection. His ideas are based on the concepts of truth, authenticity, and perfection. The conclusions he came to form the basis of western culture and were held as the absolute truth for nearly 2,000 years. Aristotle founded a planetary system and placed the earth at the center of the universe. In the second century A.D. Aristotle’s system was revised by Ptolemy. In this system, the stars and planets are attached to nine transparent crystalline spheres, each of which rotates above the earth. The ninth sphere, the primum moblie, is the closest to heaven and is, therefore, the most perfect.
http://www.angelfire.com/scifi2/zpt/ptol.html Animated GIF
Aristotle’s universe is composed of four worldly elements; earth, fire, water, and air and a fifth element which is pure, authentic, and incorruptible. The stars and planets are composed of this fifth element. Due to its proximity to heaven, this fifth element possesses God like properties and is not subject to the ordinary physical laws.
In the seventeenth century, Aristotle’s teachings were still considered to be a fundamental truth. In 1600, William Gilbert published his book “The Magnet”. Little was known of magnetism in Gilbert’s time except that it was a force that emanated from bits of lodestone. Aristotle’s influence upon Gilbert is apparent from Gilbert’s conclusion that magnetism is a result of the pure, authentic nature of lodestone. Gilbert also claimed that the earth’s magnetic field was a direct result of the pure authentic character of the deep earth. In some ways, according to the philosophy of Gilbert, the heavens, the deep earth, and lodestone were close to God.
In 1820, Hans Christian Oersted of the University of Copenhagen was demonstrating an electric circuit before his students. In Oersted’s time electrical current could only be produced by crude batteries. His battery consisted of 20 cups, each containing a dilute solution of sulfuric and nitric acid. In each cup he placed a copper and a zinc electrode. During one of the experiments he placed a compass near the apparatus. To the astonishment of his students, the compass deflected when the electric circuit was completed. Oersted had discovered that an electric current produces a magnetic field. In the nineteenth century, experiments and discoveries, like those of Oersted, began to overturn the long-held ideas of Aristotle. Gilbert’s idea that magnetism is due to a God like influence was also brought into doubt.
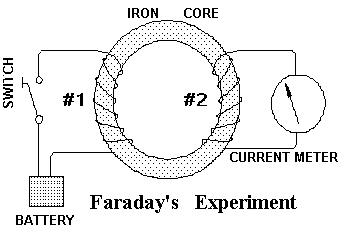
In 1824, Michael Faraday argued that if an electrical current affects a magnet then a magnet should affect an electrical current. In 1831, Faraday wound two coils on a ring of soft iron. He imposed a current on the coil #1 and he knew, from the discovery of Oersted, that the current in coil #1 would produce a magnetic field. He expected that this magnetic field would impose a continuous current in coil #2. The magnetic field did impose a current but not the continuous current that Faraday had expected. Faraday discovered that the imposed current on coil #2 appeared only when the strength of the current in coil #1 was varied.
The work of Oersted and Faraday in the first half of the nineteenth century was taken up by James Clerk Maxwell in the latter half of the same century. In 1865, Maxwell wrote a paper entitled, “The Dynamical Theory of the Electromagnetic Field”. In the paper he developed the equations that describe the electromagnetic interaction. These equations, which are based on the concept of symmetry, quantify the symmetrical relationship that exists between the electric and magnetic fields.
Maxwell’s equations show that a changing magnetic field induces an electrical field and, conversely, that a changing electrical field (a current) induces a magnetic field. Maxwell’s equations are fundamental to the design of all electrical generators and electromagnets. As such, they form the foundation upon which the modern age of electrical power was built. Maxwell was the first to quantify a basic principle of nature. In particular, he showed that nature is constructed around underlying symmetries. The electric and magnetic fields, while different from each other, are manifestations of a single, more fundamental force. The ideas of Aristotle and Gilbert about the pure, the authentic, and the incorruptible, were replaced by the concept of symmetry. Since Maxwell’s discovery, the concept that nature is designed around a deep, underlying symmetry has proven to be true time and time again. Today most advanced studies in the field of theoretical physics are based upon the principle of symmetry.
THE SYMMETRY BETWEEN FORCE AND GRAVITY
In 1687, Isaac Newton published his book, “The Principia”, in which he spelled out the laws of gravitation and motion. In order to accurately describe gravity, Newton invented the mathematics of calculus. He used his invention of calculus to recount the laws of nature. His equations attribute the gravitational force to the presence of a field. This field is capable of exerting an attractive force. The acceleration produced by this force changes the momentum of a mass.
In 1912, Albert Einstein published his “General Theory of Relativity”. The General Theory of Relativity is also a theory of gravity. Einstein’s theory, like the theory of Newton, also demonstrates that gravitational effects are capable of exerting an attractive force. This force can change the momentum of a mass. Einstein’s theory, however, goes beyond Newton’s theory in that it shows that the converse is also true. Any force which results in a change in momentum will generate a gravitational field. Einstein’s theory, for the first time, exposed the symmetrical relationship that exists between force and gravity. This concept of a gravitational symmetry was not, as in the case of the electromagnetic symmetry, universally applied. In the twentieth century, it was applied in a limited fashion by physicists in the study of gravitational waves.
http://www.angelfire.com/scifi2/zpt/images/fields.gif Pick the link to view the symmetrical relationship between the original and induced fields.
In 1989, this author wrote his first book “Elementary Antigravity”. In this book he revealed a modified model of matter. This model is based on the idea that unbalanced forces exist within matter and that these forces are the source of the gravitational field of matter. In this present work, the symmetrical relationship that exists between the forces is fully developed. The exposure of these relationships will lead to technical developments in the fields of antigravity and energy production. These developments will parallel the developments in electrical technology that occurred following Maxwell’s discovery of the symmetrical electromagnetic relationship. In review, a changing electric field (a current) induces a magnetic field and, conversely, a changing magnetic field induces an electric field. Likewise, a gravitational field induces a force and, conversely, a force induces a gravitational field.
http://www.angelfire.com/scifi2/zpt/movies/forcegr.AVI The relationship between force, gravity, and the gravitomagnetic field has been known for 100 years. This author was the first to place force in a model of matter. This author’s work is fundamental to the development of zero point technologies. This author’s work on the force/gravity symmetry was published in INFINITE ENERGY Vol. #4, Issue #22, November 1998.
To get an idea of the magnitude of the force required to produce a gravitational field, consider the gravitational field produced by one gram of matter. The amount of gravity produced by one gram of matter is indeed tiny. Now assume that this one gram of matter is converted into energy. A vigorous nuclear explosion will result. If this explosion is contained within a vessel, the outward force on the vessel would be tremendous. This is the amount of force necessary to produce the gravitational field of one gram of matter. This force is produced naturally by the mechanisms that contain the energy of mass within matter.
THE STRONG NUCLEAR FORCE AND THE NUCLEAR SPIN ORBIT SYMMETRY
A third symmetrical relationship exists between the strong nuclear force and the nuclear spin-orbit interaction. A moving nucleon induces a nuclear-magnetic field. The nuclear-magnetic field is not electromagnetic in origin. It is much stronger than the electromagnetic spin orbit interaction found within atoms. The nuclear-magnetic field tends to couple like nucleons pair wise into stable configurations. The nuclear spin orbit interaction favors nucleons with equal and even numbers of protons and neutrons. The nuclear spin-orbit interaction accounts for the fact that nucleons tend to contain the equal numbers of protons and neutrons (Z = A/2). It also accounts for the fact that nucleons with even numbers of protons and neutrons tend to be stable. The formulation of the nuclear spin orbit interaction has the same structure as electromagnetic and force-gravity interaction, however, the constants of the motion are different.
THE MATHEMATICAL RELATIONSHIPS
The next portion of this chapter is devoted to developing the mathematical relationship that exists between the forces. The reader, who is not interested in mathematical details, may skip forward to the conclusion without missing any of the chapter’s essential concepts. Following Maxwell’s laws, the known electromagnetic relationship will be derived. Then, by following the same procedure, the unknown gravitational force relationship will be found. The interaction between the strong nuclear force and the nuclear spin orbit interaction will also be explored.
# THE ELECTROMAGNETIC INTERACTION
The magnetic field produced by a changing electrical field (a current) is described by Maxwell’s electromagnetic relationship. This particular formulation, given in Equation #1, is known as Gauss’ Law. In words, Equation #1 states that the change in the number of electric flux lines passing through a closed surface is equivalent to the amount of charge that passes through the surface. The product of this charge and the electrical permittivity of free space is the current associated with the moving charge.
I = eo (d/dt) Eds
Eds
Equation #1 The current produced by an electron passing through a closed surface.
eo = the electrical permittivity of free space
I = the current in amps ; E = The electrical potential in newtons/coulomb. Note the italic bold script means that E is a vector having a magnitude and a direction.
The product of this current and the magnetic permeability of free space “uo” , yields, Equation #2, the magnetic flux through any closed loop around the flow of current.
F = (uoeo) d/dt Eds
Eds
Equation #2 The magnetic flux surrounding an electrical current.
F = the magnetic flux in Webbers ; uo = the magnetic permeability of free space
Substituting charge “q/eo” for the electrical potential yields, Equation #3.
F = (uoeo ) d(q/eo) / dt
Equation #3 The magnetic flux surrounding an electrical current.
Simplifying equation #3 yields equation #4. ( Equation #3 was simplified by taking the derivative using a mathematical operation called the chain rule. In this process eo comes out as a constant.)
F = uo (dq / dt)
Equation #4 The magnetic flux surrounding a current carrying conductor.
Equation #4 states that the magnetic flux around a conductor equals the product of the current flow ( in coulombs per second dq/dt ) and the permeability of free space.
i = (dq / dt) = (qv / L)
Equation #5 The current flow through a closed surface.
Equation #5 relates current flow “i” in coulombs per second to the product of charge “q”, velocity “v”, and the reciprocal of the distance “L” around which the charge flows. Substituting Equation #5 into Equation #4 yields Equation #6.
F = uo i
Equation #6 the magnetic flux around a current carrying conductor
Equation #6 gives the magnetic flux around a conductor carrying a constant current. The flux carries the momentum of the moving electrical charges. Its magnitude is proportional to the product of the current “i” carried in the conductor and the permeability of free space.
The derivative of Equation #6 was taken to introduce an acceleration into the system. This acceleration manifests itself as a change in the strength or direction of the current flow. This acceleration generates a second electrical field. This second electrical field contributes a force to the system. This force opposes the acceleration of the electrical charges. The electrical field described by Equation #7 expresses itself as a voltage ( joules / coulomb ) across an inductor.
E2 = uo (di / dt) ; E2 = L (di/dt) volts
Equation #7 The voltage produced by accelerating charges.
# THE GRAVITATIONAL FORCE INTERACTION
A second analysis was done. This analysis derives the relationship between gravity and a changing momentum. The analysis employs the same procedure that was used to derive the electromagnetic relationship. Disturbances in the gravitational field propagate at the speed of light. 1,2,3,4,5During the propagation interval induced fields conserve the momentum of the system. Disturbances in a gravitational system induce a gravitomagnetic field. Equation #8 is the gravitational equivalent of equation #2. Equation #8 states that the momentum of a moving mass is carried by a gravitomagnetic field. The strength of the gravitomagnetic field is proportional to the number of gravitational flux lines that pass through an infinite surface.
Fg = (uoeo) (d/dt) Egds
Egds
Equation #8 The gravito-magnetic flux surrounding moving mass
Eg The vector, gravitational potential in (newtons / kg) ; Fg = The gravitomagnetic flux
Substituting mass “m” for gravitational potential yields equation #9, is the gravitational equivalent of equation #3.
Fg = (uoeo) d (Gm) / dt
Equation #9 The gravitomagnetic flux surrounding a moving mass.
m = The mass in kg ; G = The gravitational constant
Maxwell discovered a relationship between light speed, permittivity, and permeability. This relationship is given by equation #10.
uoeo = (1 / c2)
Equation #10 Maxwell’s relationship.
Substituting Maxwell’s relationship into equation #9 yields equation #11. Equation #11 is the gravitational equivalent of Equation #4.
Fg = (G / c2) dm / dt
Equation #11 The gravitomagnetic flux surrounding a moving mass.
Equation #12 states that the mass flow “I” in kilograms per second (dm/dt) is the product of mass “m”, velocity “v”, and the length “L” of a uniform body of mass. Equation #12 is the gravitational equivalent of Equation #5. It is the gravitational mass flow.
Ig = dm / dt = mv / L
Equation #12 The mass flow through a closed surface.
Substituting #12 into Equation #11 yields Equation #13. Equation #13 is the gravitational equivalent of equation #6.
Fg = (G/c2) (mv / L)
Equation #13 The gravitomagnetic flux around a moving mass.
Fg = The gravitomagnetic field
Equation #13, the gravitomagnetic field, carries the momentum “mv” of a mass moving at a constant velocity. The magnitude of this field is proportional to the product of mass flow in kilograms per second times the ratio of the gravitation constant “G” and light speed “c” squared.
Momentum “p” is substituted for the product “mv”. Taking the derivative of the result introduces acceleration into the system. This acceleration generates a second gravitational field.

This field is given by Equation #14. This second gravitational field contributes a force to the system which opposes the acceleration of the mass.
E2g = (G / c2)( dp / dt ) / L
Equation #14
The distance “L” is the length of the moving mass “m”. In a gravitational system, this length is equivalent to the gravitational radius “r” of the mass. Substituting “r” for “L” yields equation #15. Equation #15 gives the intensity of the induced inertial force. The field described by equation #15 expresses itself as an applied force ( newtons / kilogram ).
Induced inertial force = [G / c2 r ] (dp / dt)
Equation #15 is the general formula of gravitational induction. This formula will be extensively applied in upcoming chapters.
G (the gravitational constant) = 6.67 x1011 Nm² / kg² ; c (light speed) = 3 x 108 meters / second ; (dp / dt) = the applied force in newtons ; r = the gravitational radius
# THE STRONG NUCLEAR AND NUCLEAR SPIN ORBIT INTERACTION
A third analysis was attempted . This analysis derives the relationship between the strong nuclear force and the nuclear spin-orbit interaction. This analysis employs the same procedure that was used in deriving the electromagnetic and gravitational relationships. The principle of symmetry requires a nuclear-magnetic field to be produced by the movement of nucleon. Equation #15 is the nuclear equivalent of equation #2. Equation #15 states that a change in the strong nuclear force induces a nuclear-magnetic field. The strength of this field is proportional to the number of strong nuclear flux lines that pass through an infinite surface.
Fn = (uo eo)(d/dt) Ends
Ends
Equation #15 The nuclear-magnetic (spin orbit) field
The strong nuclear force is nonlinear. The analysis cannot be fully developed. An estimate of R at the surface of a nucleon may obtained empirically.
R = 23 MeV
The nuclear field described by the equation below expresses itself as a potential ( MeV / nucleon ) associated with the spin of a nucleon.
Nuclear-magnetic energy = R d ( spin ) / dt
# CONCLUSION
Nature is constructed around underlying symmetries. The idea that nature is constructed around underlying symmetries has proven to be correct time and time again. The electro-weak theory, for example, is based on the principle of symmetry. The first natural symmetry to be discovered was the relationship between the electric and magnetic field. A second symmetrical relationship exists between force and gravity. A third symmetrical relationship exists between the strong nuclear force and the nuclear spin orbit interaction. The nature of these symmetries was explored. The mathematics used to describe the electromagnetic relationship were applied to the gravitational / force relationship. This analysis yielded (Equation #15) the general formula of gravitational induction. The mathematical analysis performed shows that gravity produces a force and conversely that a force produces gravity. Each relationship has a similar formulation and involves the element of time. The relationships differ, in that electromagnetism involves a change in the magnetic field while the gravitational/force involves a change in momentum. The nuclear spin-orbit interaction was also explored. In light of what was learned from the study of electromagnetism and gravity, it was determined that the nuclear spin-orbit interaction involves a change in the strong nuclear force.
The formulation of the each relationship is the same, however, the constants of the motion (L, G/c2, and R) are radically different. Some very profound conclusions have been obtained through the application of the simple concept of symmetry. The remainder of this text will explore, expand, and develop these constructs into a synthesis that will become the foundation of many new futuristic technologies.
http://www.angelfire.com/scifi2/zpt/images/zpe.gif A main point. Pick to view a chart that shows how the constants of the motion, discussed in this chapter, changes in a vibrationally reinforced condensate.
# NOTES
– 1. S. Kopeikin (2001), ” Testing the relativistic effect of the propagation of gravity by very long baseline interferometry “, Astrophys.J. 556, L1-L5.
– 2. T. Van Flandern (2002),
– 3. H. Asada (2002), Astrophys.J. 574, L69-L70.
– 4. S. Kopeikin (2002), .
– 5. T. Van Flandern (1998) , The speed of gravity What the experiments say², Phys.Lett.A 250, 1-11.
// end of chapter 6 …………………………………………………………………..
# Chapter 7, RESTRAINING FORCES AND MATTER
INTRODUCTION
The study of the form, function, and composition of matter has been, and continues to be, one of the greatest intellectual challenges of all time. In ancient times the Greek Empedocles (495-435 B.C.) came up with the idea that matter is composed of earth, air, fire, and water. In 430 B.C. the idea of Empedocles was rejected by, the Greek, Democritus of Abdera. Democritus believed that the substances of the creation are composed of atoms. These atoms are the smallest bits into which a substance can be divided. Any additional subdivision would change the essence of the substance. He called these bits of substance “atomos” from the Greek word meaning “indivisible”. Democritus was, of course, correct in his supposition, however, at the time, no evidence was available to confirm this idea. Ancient technology was primitive and could not to confirm or contest any of these ideas. Various speculations of this sort continued to be offered and rejected over the next 2,000 years.
The scientific revolution began in the seventeenth century. With this revolution came the tools to test the theories of matter. By the eighteenth century these tools included methods of producing gases through the use of chemical reactions, and the means to weigh the resultant gases. From his studies of the gaseous by-products of chemical reactions, French chemist Antoine Lavoisier (1743-1794) discovered that the weight of the products of a chemical reaction equals the weight of the of the original compound. The principle of “the conservation of mass” was born. For his achievements Lavoisier is today known as the father of modern chemistry.
Late in the eighteenth century, the first use of another new tool began to be applied to test the theories of matter. This tool is electrical technology. The first electrical technology to be applied to the study of matter, electrolysis , involves the passing of an electrical current through a conductive solution. If an electrical current is passed through a conductive solution, the solution tends to decompose into its elements. For example, if an electric current is passed through water, the water decomposes, producing the element hydrogen at the negative electrode and the element oxygen at the positive electrode. With the knowledge obtained from the use of these new technologies, English schoolteacher, John Dalton (1766-1844) was able to lay down the principles of modern chemistry. Dalton’s theory was based on the concept that, matter is made of atoms, all atoms of the same element are identical, and atoms combine in whole number ratios to form compounds.
Electrical technology became increasingly more sophisticated during the nineteenth century. Inventions such as the cathode ray tube (a television picture tube is a cathode ray tube) allowed atoms to be broken apart and studied. The first subatomic particle to be discovered was the electron. In 1897, J.J. Thomson demonstrated that the beams seen in cathode ray tubes were composed of electrons. In 1909, Robert Millican measured the charge of the electron in his, now famous, oil drop experiment. Two years later, Ernest Rutherford ascertained the properties of the atomic nucleus by observing the angle at which alpha particles bounce off of the nucleus. Niels Bohr combined these ideas and in 1913, placed the newly discovered electron in discrete planetary orbits around the newly discovered nucleus. The planetary model of the atom was born. With the appearance of the Bohr model of the atom, the concept of the quantum nature of the atom was established.
http://www.angelfire.com/scifi2/zpt/images/bohr.gif Pick the link to view the Bohr model of the atom.
THE QUANTUM MYSTERY
As the temperature of matter is increased, it emits correspondingly shorter wavelengths of electromagnetic energy. For example, if a metal poker is heated it will become warm and emit long wavelength infrared heat energy. If the heating is continued the poker will eventually become red hot. The red color is due to the emission of shorter wavelength red light. If heated hotter still, the poker will become white hot emitting even shorter wavelengths of light. An astute observer will notice that there is an inverse relationship between the temperature of the emitter and the wavelength of the emission. This relationship extends across the entire electromagnetic spectrum. If the poker could be heated hot enough it would emit ultra-violet light or X-rays.
The German physicist Max Karl Ludwig Planck studied the light emitted from matter and came to a profound conclusion. In 1900, Planck announced that light waves were given off in discrete particle-like packets of energy called quanta. Today Planck’s quanta are know known as photons. The energy in each photon of light varies inversely with the wavelength of the emitted light. Ultraviolet, for example, has a shorter wavelength than red light and, correspondingly, more energy per photon than red light. The poker, in our example, while only red hot cannot emit ultraviolet light because its’ atoms do not possess enough energy to produce ultraviolet light. The sun, however, is hot enough to produce ultraviolet photons. The ultraviolet photons emitted by the sun contain enough energy to break chemical bonds and can “sun” burn the skin. The radiation spectrum cannot be explained by any wave theory. This spectrum can, however, be accounted for by the emission of a particle of light or photon. In 1803, Thomas Young discovered interference patterns in light. Interference patterns cannot be explained by any particle theory. These patterns can, however, be accounted for by the interaction of waves. How can light be both a particle and a wave?
In 1924, Prince Louis de Broglie proposed that matter possess wave-like properties. 1According to de Broglie’s hypothesis, all moving matter should have an associated wavelength. De Broglie’s hypothesis was confirmed by an experiment conducted at Bell Labs by Clinton J. Davisson and Lester H. Germer. In this experiment an electron beam was bounced off of a diffraction grating. The reflected beam produced a wave like interference pattern on a phosphor screen. The mystery deepened; not only does light possess particle-like properties but matter possesses wave-like properties. How can matter be both a particle and a wave?
http://www.angelfire.com/scifi2/zpt/images/germar.gif Pick the link to view one form of the Germar Davisson experiment.
THE GREAT MISTAKE
Throw a stone in a lake and watch he waves propagate away from the point of impact. Listen to a distant sound that has traveled to you from its source. Shake a rope and watch the waves travel down the rope. Tune in a distant radio station, the radio waves have traveled outward from the station to you. Watch the waves in the ocean as they travel into the shore. In short, waves propagate, its their nature to do so, and that is what they invariably do. Maxwell’s equations unequivocally demonstrate the fields propagate at light speed. Matter waves, however, remain “stuck” in the matter. Why do they not propagate? What “sticks” them? An answer to this question was presented by Erwin Schrödinger and Werner Heisenberg at the Copenhagen conventions. The Copenhagen interpretation states that elementary particles are composed of particle-like bundles of waves. These bundles are know as a wave packets. The wave packets move at velocity V. These wave packets are localized (held is place) by the addition of an infinite number of component waves. Each of these component waves has a different wavelength or wave number. An infinite number of waves each with a different wave number is required to hold a wave packet fixed in space. This argument has two major flaws. It does not describe the path of the quantum transition and an infinite number of real component waves cannot exist within a finite universe.
Max Born attempted to side step these problems by stating that the wave packets of matter are only mathematical functions of probability. Only real waves can exist in the real world, therefore an imaginary place of residence, called configuration space, was created for the probability waves. Configuration space contains only functions of kinetic and potential energy. Forces are ignored in configuration space.
“Forces of constraint are not an issue. Indeed, the standard Lagrangian formulation ignores them…In such systems, energies reign supreme, and it is no accident that the Hamiltonian and Lagrangian functions assume fundamental roles in a formulation of the theory of quantum mechanics..” Grant R. Fowles University of Utah
Ordinary rules, including the rules of wave propagation, do not apply in configuration space. The propagation mystery was supposedly solved. This solution sounds like and has much in common with those of the ancient philosophers. It is dead wrong!
“Schrödinger never accepted this view, but registered his concern and disappointment that this transcendental, almost psychical interpretation had become universally accepted dogma.” Modern Physics Serway, Moses, Moyer; 1997
Einstein also believed that something was amiss with the whole idea. His remark, “God does not play dice” indicates that he placed little confidence in these waves of probability. For the most part, the error made little difference, modern science advanced, and bigger things were discovered. It did, however, make at least one difference; it forestalled the development of gravitational and low level nuclear technologies for an entire Century.
THE CORRECTION
Matter is composed of energy and fields of force. Matter can be mathematically modeled but a mathematical model does not make matter. Matter waves are real, they contain energy, are the essence of mass, and convey momentum. Disturbances in the force fields propagate at light speed.
” This result is rather surprising… since electrons are observed in practice to have velocities considerably less than the velocity of light it would seem that we have a contradiction with experiment.
Paul Dirac, his equations suggested that the electron propagates at light speed. 11″
Matter does not disperse because it is held together by forces. These forces generate the gravitational field of matter, establish the inertial properties of matter, and set matter’s dynamic attributes. The understanding of the nature of the restraining forces provides insight of the quantum transition. The remainder of this chapter will be spent qualifying these forces and the relationship that they share with matter. The ideas to follow are central to this author’s work. Reader’s who have no interest in math may skip to the conclusion without missing the essential details of this chapter. Essentially the math shows that forces within matter are responsible for many of the properties of matter.
This concept will be extended in Chapter 10. The various fields that compose matter have radically different ranges and strengths. The force, that pins the various fields within matter, is generated when the amplitude of a field exceeds the elastic limit of space.
GRAVITIONAL MASS
A version of this section was published in “Infinite Energy” Vol 4, #22 1998
The matter wave function is composed of various fields. Photons were employed to represent these various fields. Photons exhibit the underlying relationship between momentum and energy of a field (static or dynamic) in which disturbances propagate at luminal velocities. Consider photons trapped in a massless perfectly reflecting box. The photon in a box is a simplistic representation of matter. Light has two transverse modes of vibration and carries momentum in the direction of its travel. All three modes need to be employed in a three dimensional model. For the sake of simplicity this analysis considers only a single dimension. The photons in this model represents the matter wave function and the box represents the potential well of matter. As the photons bounce off of the walls of the box momentum “p” is transferred to the walls of the box. Each time a photon strikes a wall of the box it produces a force. This force generates the gravitational mass associated with the photon in the box. The general formula of gravitational induction, as presented in the General Theory of Relativity 3, 4(this equation was derived in Chapter 6) is given by Equation #2.
Eg = G / (c2r) (dp / dt)
Equation # 2 The gravitational field produced by a force
Eg = the gravitational field in newtons / kg ; G = the gravitational constant ; r = the gravitational radius ; dp/dt = force
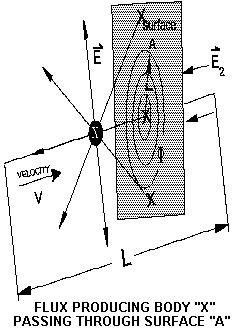
Each time the photon strikes the wall of the box it produces a gravitation field according to equation #2. The gravitational field produced by an impact varies with the reciprocal of distance “1/r”. The gravitational field produced by matter varies as the reciprocal of distance squared “1/r2”. This author has ascertained how the “1/r2” gravitational field of is produced by a force. It will now be shown that the superposition of a positive field that varies with an “1/r” rate over a negative field that varies with an “1/r” rate, produces the “1/r2” gravitational field of matter. An exact mathematical analysis of the gravitational field produced by the photon in the box will now be undertaken.
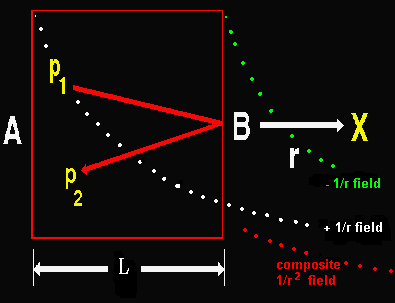
L = The dimensions of the box ; p = momentum ; t = the time required for the photon to traverse the box=L/c ; r = the distance to point X
The far gravitational field at point X is the vector sum of the fields produced by the impacts on walls A and B.
This field is given below.
Eg at x = 1/r field from wall A – 1/r field from wall B
Equation 3 Showing the super-position of two fields.
Eg at x = (G / [ c2 (r+L) ] ) ( dp / dt ) – (G / [c2r] ) (dp / dt)
Equation 4 Simplifying.
Eg at x = – (G / c2) (dp / dt) [ L / (r2 + r L) ]
Equation 5 Taking the limit to obtain the far field.
Eg at x = limas r>>L – (G / c2) (dp / dt) [ L / (r2 + r L) ]
The result , Equation #7, is the far gravitational field of matter. Far, in this example, means greater than the wavelength of an elementary particle. In the case of a superconductor far means longer than the length of the superconductor.
Eg at x = – (G / c2) (dp / dt) L / r2 Equation #7
This momentum of an energy field that propagates at light speed is given by the equation below 2 .
p = E / c ; E = the energy of the photon ; c = light speed ; p = momentum (radiation pressure)
The amount of force (dp / dt) that is imparted to the walls of the box depends on the dimensions of the box L. Equation 8 gives the force on the walls of the box.
dp / dt = Dp / Dt = (2E / c) / (L / c) = 2E / L Equation #8
Equation #8 was substituted into Equation #7 and a factor of 1/2 was added. The factor of 1/2 is required because the resultant field is produced by two impacts and the energy can only impact one wall at a time. Equation 9 The far gravitational field produced by energy bouncing in a box
Eg at x = – (1/2) (G / c2) (2E / L) (L / r2) Equation #9
Equation 10 is Einstein’s relationship between matter and energy. M = E / c2 Equation #10
Substituting mass for energy yileds Equation #11, Newton’s formula for gravity. 5
Eg at x = – GM / r2 Equation #11
This analysis clearly shows that unbalanced forces within matter generate the gravitational field of matter. 6, 10 These forces result from the impact of energy which flows at luminal velocities.
# MATTERS deBroglie WAVELENGTH
Note: a version of this section was published in “The Journal of New Energy” Vol 5, September 2000
In 1924 Prince Louis DeBroglie proposed that matter has a wavelength associated with it. 1 Schrödinger incorporated deBroglie’s idea into his his famous wave equation. The Davission and Germer experiment demonstrated the wave nature of the the electron. The electron was described as both a particle and a wave. The construct left many lingering questions. How can the electron be both a particle and a wave? Nick Herbert writes in his book “Quantum Reality” Pg. 46;
The manner in which an electron acquires and possesses its dynamic attributes is the subject of the quantum reality question. The fact of the matter is that nobody really these days knows how an electron, or any other quantum entity, actually possesses its dynamic attributes.”
Louis deBroglie suggested that the electron may be a beat note. 7 The formation of such a beat note requires disturbances to propagate at light speed. Matter propagates at velocity V. DeBroglie could not demonstrate how the beat note formed. This author’s model demonstrates that matter vibrates naturally at its Compton frequency . A standing Compton wave is pinned in place at the elastic limit of space ( Chapter 10 ). A traveling wave component is associated with moving matter. The traveling wave component bounces off the discontinuity produced at the elastic limit of space . The reflected wave doppler shifts as it bounces of off the discontinuity. The disturbances propagate at luminal velocities. They combine to produce the dynamic DeBroglie wavelength of matter. The animation shows the DeBroglie wave as the superposition of the original and the Doppler shifted waves.
http://www.angelfire.com/scifi2/zpt/Waves.html Pick the link to view a JAVA animation on the DeBroglie wavelength of matter.
The harmonic vibration of a quantum particle is expressed by its Compton wavelength. Equation #1A expresses the Compton wavelength.
lc = h / Mc
Equation #2A gives the relationship between frequency f and wavelength l. Please note that the phase velocity of the wave is c.
c = f l
Substituting Eq #2A into Eq. #1A yields Eq #3A the Compton frequency of matter.
fc = Mc2 / h
A doppler shifted component of the original frequency is produced by the reflection at matter’s surface. Classical doppler shift is given by Eq #4A.
f2 = f1 ( 1 +- v / c)
A beat note is formed by the mixing of the doppler shifted and original components. This beat note is the deBroglie wave of matter.
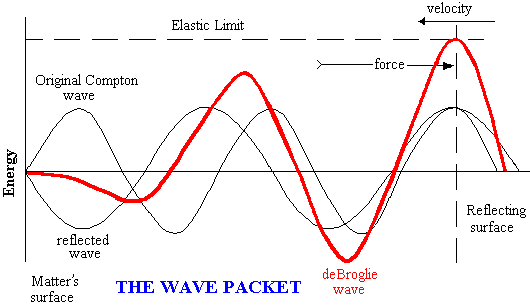
Equation #5A and the above express a function “F” involving the sum of two sin waves.
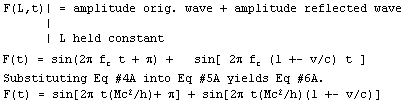
Refer to the figure above. A minimum in the beat note envelope occurs when the component waves are opposed in phase. At time zero the angles differ by p radians. Time zero is a minimum in the beat note envelope. A maximum in the beat envelope occurs when the component waves are aligned in phase. The phases were set equal, in Equation #7A, to determine the time at which the aligned phase q condition occurs.
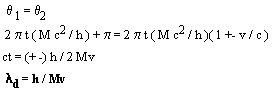
The result, Equation #10A, is the deBroglie wavelength of matter. Reflections result from a containment force. These reflections combine to produce the deBroglie wavelength of matter.
INERTIAL MASS
An analysis was done that described inertial mass in terms of a restraining force. This force restrains disturbances that propagate at luminal velocities. Consider energy trapped in a perfectly reflecting containment. (see the figure below)

This energy in a containment model is a simplistic representation of matter. In this analysis no distinction will be made between baryonic, leptonic, and electromagnetic waves.
The wavelength of the energy represents the Compton wavelength of matter. The containment represents the surface of matter. The field propagates at light speed. Its momentum is equal to E/c. The containment is at rest. The energy is ejected from wall “A” of the containment, its momentum is p1. The energy now travels to wall “B”. It hits wall B and immediately bounces off. Its momentum is p2 . The energy now travels back to wall “A”, immediately bounces off, its momentum is again p1. This process repeats continuously. If the energy in the containment is evenly distributed throughout the containment, the momentum carried by this energy will be distributed evenly between the forward and backward traveling components. The total momentum of this system is given in equation #1C.
pt =(p1 /2 – p2 /2)
The momentum of a flow of energy is given by equation #2C
p = E/c (Eq #2); E = energy ; c = light speed ; p = momentum
Substituting Eq. #2C into Eq. #1 yields Eq. #3C.
pt= [E1 /2c – E2/2c] ; ( Eq. #3C)
Given the containment is at rest. The amount of energy in the containment remains fixed, the quantity of energy traveling in the forward direction equals the quantity of energy traveling in the reverse direction. This is shown in equation #4.
E1= E2;(Eq #4C)
Substituting Eq. #4C into Eq. #3C yields Eq #5C.
pt =(E/2c)(1 – 1) ; (Eq #5C)
Equation #5 is the total momentum of the system at rest. If an external force is applied to the system its velocity will change. The forward and the reverse components of the energy will then doppler shift after bouncing off of the moving containment walls. The momentum of a an energy flow varies directly with its frequency. Given that the number of quantums of energy is conserved, the energy of the reflected quantums varies directly with their frequency. This is demonstrated by equation #6C.
E2= E(1) [ff / fi]; (Eq. #6C)
Substituting Eq. #6C into Eq #5C. yields eq. #7C.
pt = E/2c)[(ff1/fi1) – (ff2 /fi2)] ; (Eq #7C)
Equation #7C is the momentum of the system after all of its energy bounces once off of the containment walls. Equation #7 shows a net flow of energy in one direction. Equation #7C is the momentum of a moving system. The reader may desire to analyze the system after successive bounces of its energy. This analysis is quite involved and unnecessary. Momentum is always conserved. Given that no external force is applied to the system after the first bounce of its energy, its momentum will remain constant.
Relativistic doppler shift is given by equation #8C.
(ff / fi) = [1 – v2 / c2]1/2 / (1 +- v/c), Eq #8C ; v = velocity with respect to the observer ; c = light speed ; ff/fi = frequency ratio ; + or – depends on the direction of motion
Substituting equation #8 into equation #7C yields equation 9C
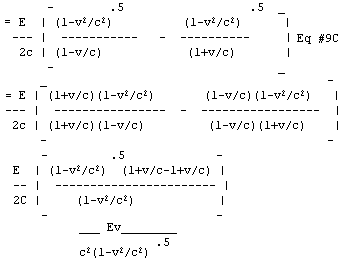
Substituting mass for energy, M = E/c2
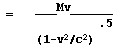
The result, equation #14C is the relativistic momentum of moving matter. This first analysis graphically demonstrates that inertial mass is produced by a containment force at the surface of matter. A fundamental change in the frame of reference is produced by the force of containment. This containment force converts energy, which can only travel at light speed, into mass, which can travel at any speed less than light speed. 8
# A RECONCILIATION OF QUANTUM PHYSICS AND SPECIAL RELATIVITY
Note: A version of this analysis has been published in this author’s book Elementary Antigravity , Vantage Press 1989, ISBN 0-533-08334-6
According to existing theory the matter wave emerges from the Fourier addition of component waves. This method requires an infinite number of component waves. Natural infinities do not exist within a finite universe. The potential and kinetic components of a wave retain their phase during a Fourier localization. The aligned phase condition is a property of a traveling wave. The Fourier process cannot pin a field or stop a traveling wave.
Texts in quantum physics commonly employ the Euler formula in their analysis. The late Richard Feynman said, “The Euler formula is the most remarkable formula in mathematics. This is our jewel.” The Euler formula is given below:
e i q = cosq + i sinq
The Euler formula describes the simple harmonic motion of a standing wave. The cos component represents the potential energy of a standing wave. The sin component represents the kinetic energy of a standing wave. The kinetic component is displaced by 90 degrees and has a i associated with it. The localization of a traveling wave through a Fourier addition of component waves is in error. To employ this method of localization and then to describe the standing wave with the Euler formula is inconsistent. This author corrected this error through the introduction of restraining forces. The discontinuity produced at the elastic limit of space restrains the matter wave. The potential and kinetic components of the restrained wave are displaced by 90 degrees. A mass bouncing on the end of a spring is a good example of this type of harmonic motion. At the end of it travel the mass has no motion ( kinetic energy = zero) and the spring is drawn up tight ( potential energy = maximum ). One quarter of the way into the cycle the spring is relaxed and the mass is moving at its highest velocity (kinetic energy = maximum). A similar harmonic motion is exhibited by the force fields. The energy of a force field oscillates between its static and magnetic components.
For some motion music click on the moving mass.
Mass energy ( Em ) is a standing wave. A standing wave is represented on the -j axis of a complex plane.
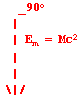
The phase of a standing wave is 90 degrees. All standing waves are localized by restraining forces.
A traveling wave has its kinetic and potential components aligned in phase. An ocean wave is a good example of this type of harmonic motion. The wave’s height ( potential energy ) progresses with the kinetic energy of the wave.
The energy “E” contained by a wave carrying momentum “P” is expressed below.
E = Pc
The traveling wave expresses itself through its relativistic momentum “P”.
P = Mv / (1- v2 / c 2 )1/2
Substituting yields the amount of energy that is in motion “Eq“. Energy flows are represented on the X axis of a complex plane.
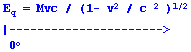
The vector sum of the standing ( Em ) and traveling ( Eq ) components equals the relativistic energy ( Er ) of moving matter.
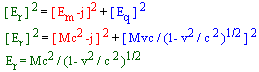
The relativistic energy is represented by the length of the hypotenuse on a complex plain
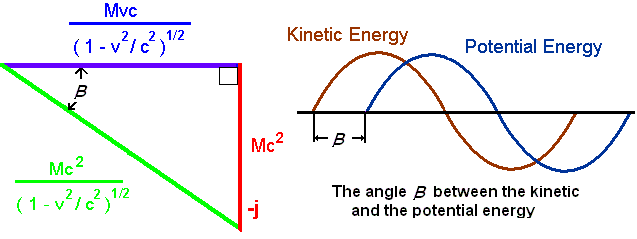
The ratio of standing energy to the relativistic energy [ Em / Er ] reduces to (1- v2 / c 2 )1/2. This function express the properties of special relativity. The arc sin of this ratio is the phase;
b = arc sin (1- v2 / c 2 )1/2
The phase b expresses the angular separation of the potential and kinetic energy of matter. The physical length of a standing wave is determined by the spatial displacement of its potential and kinetic energy. This displacement varies directly with the phase b. The phase b varies inversely with the group velocity of the wave. This effect produces the length contraction associated with special relativity.
Time is represented on the Z (out of the plain) axis on a complex diagram. The rotation of a vector around the X axis into the Z axis represents the change in potential energy with respect to time. The rotation of a vector around the Y axis into the Z axis represents a change in potential energy with respect to position. Relativistic energy is reflected on both axes. The loss in time by the relativistic component Er is compensated for by gain in position.
The phase b of a wave expresses the displacement of its potential and the kinetic energy. When placed on a complex diagram the phase directly determines the relativistic momentum, mass, time, and length. These effects reconcile special relativity and quantum physics.
The analysis reveals information not provided by special relativity. The ratio of traveling energy to the relativistic energy ( Eq / Er ) reduces to v/c. The simplicity of the ratio suggests that it represents a fundamental property of matter. In an electrical transmission line this ratio is known as the power factor. The power factor is a ratio of the flowing energy to the total energy. The construct of Special Relativity may be derived a-priori from the premice that the group velocity of the matter wave is V and the phase velocity of the matter wave is c. The difference between these two velocities is produced by reflections. Reflections result from restraining forces. The same principles apply to all waves in harmonic motion.
This model requires a restrained matter wave function. What is the nature of this restraing force? Are forces beyond the four known forces required? This author will show that no addtional forces are requied. The restraining force is produced throgh the action of the known forces. The nature of this restraining force will be presented in Chapter 10. An analysis of this restraining force, in Chapter 12, revealed the path of the quantum transition.
This model produces a second result. This result contains negative mass with a lagging phase angle. It is located along the +j axis. Is this second result that of anti-matter? Capacitors are used to cancel reactance along a power line. On the complex plane the capacitance at vector -j cancels out the reactance at vector +j leaving only the X axis traveling wave component. Is this what occurs when matter meets antimatter? This author believes that matter’s leading power factor ( kinetic energy leads potential energy) is an affect of a elastic anomaly. This anomaly is associated with the restraint of the wave function. These ideas will be developed in Chapters 10 and 11.
# THE GRAVITATIONAL AFFECT OF PHOTONS
Einstein’s principle of equivalence states that gravitational and inertial mass are always in proportion. The photon has no rest mass and a fixed inertial mass. What is its gravitational mass? General relativity states that gravity warps space. Photons take the quickest path through this warped space. The path of a photon is effected by gravity. The effect has been measured. The light of star was bent as it passed near the sun. The momentum of the light was altered. The principle of the conservation of momentum requires that the sun experiences an eqivalent change in momentum. The bending light must generate a gravitational field that pulls back on the sun. Bending light has a gravitational mass.
Photons from the extremes of the universe have traveled side by side for billions of years. These photons do not agglomerate. The slightest agglomeration would result in a decrease in entropy. This decrease would be in violation of the laws of thermodynamics. Photons traveling in a parallel paths extert no gravitational influence upon each other.
Matter gives up energy during the process of photon ejection. The principle of the conservation of energy requires that the negative gravitational potential and the positive energy of the universe remain in balance. The ejected photon must carry a gravitational mass that is equivalent to the gravitational mass lost by the particle.
These conditions are satisfied with a variable gravitational mass. The gravitational mass of the photon varies directly with the force it experiences. This force is expressed as a changing momentum (dp/dt).
Hubbles’ constant expresses the expansion space in units of 1/time. Ordinarily, the effects resulting for the Hubble expansion are quite tiny. At great distances and at high velocities significant effects do, however, take place. As a photon travels through space at the high velocity of light it red shifts. This red shift may be considered to be the result of an applied force. This force is produced by the acceleration given in equation #1D.
Acceleration = Hc Eq #1D ; H = Hubble’s constant, given in units of (1/sec) ; c = light speed
To demonstrate the gravitational relationships of a photon the principle of the conservation of momentum will be employed. According to this principle exploding bodies conserve there center of gravitational mass. Mass M ejects a photon while over the pivot I. The gravitational center of mass must remain balanced over the pivot point I. Mass M is propelled to the left velocity at v1 and the photon travels to the right at velocity c. The product of the velocity and time is the displacement S.
Setting the products of the displacements S and the gravitational masses
Mg equal yields equation #2D.
Mg1 S1= Mg2 S2 ; Eq #2D
The general formula of gravitational induction, as presented in the General Theory of
Relativity 3, 4 ( this equation was derived in Chapter 6 ) is substituted for the gravitational mass of the photon on right side of the equation below.
GMS /r2 = (G/c2) (force) S /r2
GMS /r2= (G/c2) dp/dt S /r2
GM(v1 t) = (G/c2) dp/dt (ct)r ; Eq #5D
Substituting, dp/dt = Ma = MHc = (E/c2)Hc = EH/cEq #6D
G(Mv1)t = (G/c2 )( E / c) Hctr
Substituting momentum p for Mv1 and E/c
Gp1 t = (G/c2)p2 Hctr
Setting the momentums equal. p1= p2
c = Hr ; Eq #11D
The result, equation #11D, shows that the gravitational mass of a photon is generated by the force it experiences as it accelerates through Hubble’s constant. The result is true only under the condition where the speed of light is equal to the product of Hubble’s constant and the radius of the universe. This qualification is essentially consistent with the measured cosmological values. The radius and expansion rate are independent properties of this universe. The speed of light and the gravitational constant G are dependent upon these properties. It will be shown in upcoming chapters that the values of the natural constants are dependent upon the mass, radius, and expansion rate of the universe. 12The gravitational radius of the photon is the radius of the universe. On the largest scales the gravitational effect of photonic energy is equal to the gravitational effect of mass energy. The result demonstrates that the negative gravitational potential and the positive energy of the universe remain in balance.
# Schrödinger’s Wave Equation Revisited
Schrödinger’s wave equation is a basic tenement of low energy physics. It embodies all of chemistry and most of physics. The equation is considered to be fundamental and not derivable from more basic principles. The equation will be produced (not derived) using an accepted approach. Several assumptions are fundamental to this approach. The flaws within these assumptions will be exposed.
This author will derive Schrödinger’s wave equation using an alternate approach. It will be shown that Schrödinger’s wave equation can be fundamentally derived from the premice that the phase velocity of the mater wave is luminal. Restraining forces confine the luminal disturbances. The new approach is fundamental and yields known results.
# The accepted approach
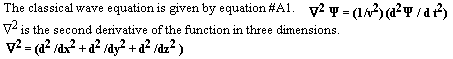
The wave equation describes a classical relationship between velocity, time, and position. The velocity of the wave packet is v. It is an error to assume that the natural velocity of a matter wave is velocity v. Disturbances within force fields propagate at light speed c. The matter wave Y is also a field. Like all fields it propagates at velocity c. Equation #3 below expresses the wave equation as of function of position and time.
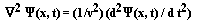
The exponential form of the sin function (e jwt ) is introduced. This function describes a sin wave. The j in the exponent states that the wave contains real and imaginary components. The potential energy of wave is represented by the real component and the kinetic energy of a wave is represented by the imaginary component. In a standing waves these components are 90 degrees out of phase. Standing waves are produced by reflections. The required reflections are not incorporated within current models. Current models include (e jwt ) ad-hoc.
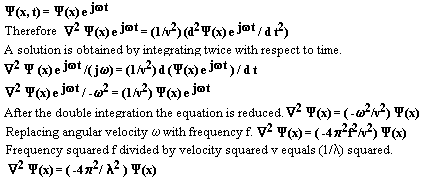
The deBroglie relationship is introduced. It is also incorporated ad-hoc. The introduction of the deBroglie wave was questioned by Professors Einstein and Langevin. H. Ziegler pointed out in a 1909 discussion with Einstein, Planck, and Stark that relativity would be a natural result if all of the most basic components of mass moved at the constant speed of light. 13This author’s work is based on the premice that disturbances in the force fields propagate at light speed. This analysis has shown that the deBrogle wavelength is a beat note. This beat note is generated by a reflection of a matter’s Compton wave. Disturbances in the the Compton wave propagate at luminal velocity.
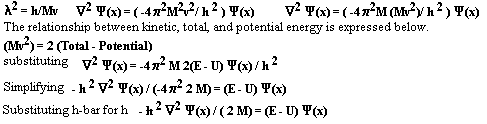
The result below is the time independent Schrödinger equation. The Schrödinger equation states that the total energy of the system equals the sum of its kinetic and potential energy. Energy is a scalar quantity. Scalar quantities do not have direction. This type of equation is known as a Hamiltonian. The Hamiltonian ignores restraining forces. The unrestrained matter wave propagates at velocity v. It is an error to assume that an unrestrained wave propagates without dispersion.
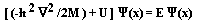
A new approach
The phase velocity of the matter wave is c. The matter wave is pinned into the structure of matter by restraining forces. The resultant force has a magnitude and a direction. The solution is Newtonian. The superposition of the Compton wave and its doppler shifted reflection is the deBrogle wavelength of matter.
The electrons natural vibrational frequency was determined in Chapter 10 of this text. This frequency is known as the Compton frequency of the electron.
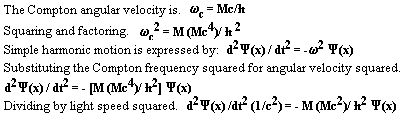
Refer to equation A1. Substituting Ñ2 for acceleration divided by light speed squared. This step embodies the idea the disturbances in the matter wave propagate at luminal velocities.
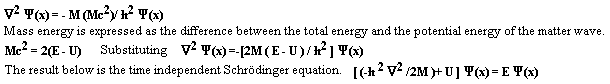
The time independent Schrödinger equation has been derived from a simple technique. It has been demonstrated that the matter wave contains the forces of nature. Disturbances within these fields propagate at luminal velocities. Restraining forces prevent dispersion. This influence extends through the atomic energy levels.
NEW TECHNOLOGIES
The movement of ordinary matter does not produce a net magnetic field. The movement of charged matter does produce a net magnetic field. Charged matter is produced by the separation of positive and negative charges. The derivation used to develop Newton’s formula of gravity (Equation #3) shows that matter may harbor positive and negative near field gravitational components.
The wavefunctions of superconductors are collimated. The collimated wave functions act in unison like a single macroscopic elementary particle. The near field gravitational components of a superconductor are macroscopic in size. The rotation of these local gravitational fields is responsible for the gravitational anomaly observed at Tampere University. 9
CONCLUSION
The forces of nature are pinned into the structure of matter by forces. Forces generate the gravitational mass of matter, determine matter’s relativistic properties, and determine matter’s dynamic properties. The nature of the bundling force will be presented in Chapters 10 & 11. The understanding of the nature of the bundling force reveals the path of the quantum transition.
NOTES
– 1.French aristocrat Louis de Broglie described the electrons wavelength in his Ph. D. thesis in 1924. De Broglie’s hypothesis was verified by C. J. Davisson and L. H. Germer at Bell Labs.
– 2.Gilbert N. Lewis demonstrated the relationship between external radiation pressure and momentum.Gilbert N. Lewis.Philosophical Magazine, Nov 1908.
– 3.A. Einstein, Ann d. Physics 49,1916.
– 4.Einstein’s principle of equivalence was experimentallyconfirmed byR.v.Eötös in the 1920’s. R.v.Eötös,D. Pekar,and Feteke,Ann. d. Phys 1922.
Roll, Krotkov and Dicke followed up on the Eötvös experiment and confirmed the principle of equivalence to and accuracy of one part in 10 11in the 1960’s.
R.G. Roll,R.Krokow&Dicke,Ann.of Physics 26,1964.
– 5.Sir. Issac Newton,PHYILOSOPHICA NATURALIS PRINCIPIA MATHENATICA (1687).
– 6. Jennison, R.C. “What is an Electron?”Wireless World, June 1979. p. 43.
“Jennison became drawn to this model after having experimentally demonstrated the previously unestablished fact that a trapped electromagnetic standing wave has rest mass and inertia.”
Jennison & Drinkwater Journal of Physics A, vol 10, pp.(167-179) 1977
Jennison & Drinkwater Journal of Physics A, vol 13, pp.(2247-2250)1980
Jennison & Drinkwater Journal of Physics A, vol 16, pp.(3635-3638)1983
– 7.B. Haisch & A. Rueda of The California Institute for Physics and Astrophysics have also developed the deBroblie wave as a beat note.Refer to:
http://www.calphysics.org/mass.html
http://xxx.lanl.gov/abs/gr-qc/9906084
– 8.Znidarsic F. ” The Constants of the Motion ” The Journal of New Energy. Vol. 5, No. 2 September 2000
– 9.”A Possibility of Gravitational Force Shielding by Bulk YBa2Cu307-x”, E. Podkletnov and R. Nieminen,Physica C, vol 203, (1992), pp 441-444.
– 10.Puthoff has shown that the gravitational field results from the cancellation of waves.This author’s model is an extension version this idea.
H.E. Puthoff, ” Ground State Hydrogen as a Zero-Point-Fluctuation-Determined State “, Physical Review D, vol 35, Number 3260, 1987
H. E. Puthoff ” GRAVITY AS A ZERO-POINT FLUCTUATION FORCE “, Physical Review A, vol 39, Number 5, March 1989
– 11.Ezzat G. Bakhoum ” Fundamental disagreement of Wave Mechanics with Relativity “, Physics EssaysVolume 15, number 1, 2002
– 12.John D. Barrow and John K. Webb” Inconstant Constants “, Scientific AmericanJune 2005
– 13.Albert Einstein, ” Development of our Conception of Nature and Constitution of Radiation “, Physikalische Zeitschrift 22 , 1909.