### Haisch, Bernhard : (page created at November 2007 update)
## REPLY TO MICHEL’S ‘COMMENT ON ZERO-POINT FLUCTUATIONS AND THE COSMOLOGICAL CONSTANT’, BERNHARD HAISCH from ‘ZPF_APJ.PDF’ 3 pages, 159kb.
THE ASTROPHYSICAL JOURNAL, 488:563È565, 1997 October 20, 1997. The American Astronomical Society. All rights reserved. Printed in U.S.A.p.563-565
Bernhard Haisch ;Solar and Astrophysics Laboratory, Lockheed Martin, 3251 Hanover Street, Palo Alto, CA 94304; and Max-Planck-Institut fur extraterrestrische Physik, D-85740 Garching, Germany.
and ALFONSO RUEDA ; Departments of Electrical Engineering and Physics, California State University, Long Beach, CA 90840. Received 1997 February 3; accepted 1997 May 29
Abstract: Michel has attempted to dismiss the concept of a vacuum electromagnetic zero-point Ðeld (ZPF) as a ‘computational trick.’ He criticizes the work of several researchers, and specifically the Rueda, Haisch & Cole proposal that, ‘the ZPF may have something to do with cosmic voids’ and their reference to ‘various other publications suggesting still other physical applications.’ We interpret the latter as referring principally to our proposition that the ZPF underlies the origin of inertia. If that concept proves to be true and a new relativistic derivation increases our confidence its implications would solve one of Michel’s major concerns: the cosmological constant problem. In this reply we thus seek to balance the perspective presented to the astrophysical community by Michel.
Subject headings : cosmology: theory È elementary particles È gravitation È MHD È relativity
1 – Introduction:
We suggest that the attempt by to dismiss Michel (1996) the concept of a vacuum electromagnetic zero-point Field (ZPF) as a ‘computational trick’ is not prudent. The enormous success of quantum theory notwithstanding, the same accusation could equally be leveled against it. We say this not to discredit quantum theory but merely to level the Field for an even-handed consideration of the semiclassical ZPF approach forming the basis of stochastic electrodynamics (SED) which Michel criticizes. From popular-level books to advanced textbooks the message is the same and has not changed in essence since Bohr: quantum methods work, and that is all one can legitimately demand. Consider, for example, what Davis & Betts (1994) have to say in paragraph 1.5 oftheir textbook: ‘The electron itself is not a wave. Rather, the way it moves about is controlled by wave-like principles.
Physicists still regard an electron as a point-like entity but the precise location of that point may not be well-defined. What, then, are these matter waves? They are not waves of any substance but are abstract waves.’
A wave function, or equivalently a state in a Dirac vectorspace representation, is a successful but purely mathematical device for predicting the results of measurements.
Everyone agrees that a wave function or vector state can be associated with a particle, but no one knows what the physical nature of this association is. Whether one characterizes this computational basis either of quantum theory or of SED as ‘methodology’ or ‘trick’ becomes a matter of polemics.
The motivation for pursuing SED heretofore has been to try to develop a classical basis for quantum laws in which fluctuations of a real electromagnetic ZPF acting as a random background interact with and perturb charged particles.
Such perturbations generate quantum-like behavior. One can understand why Michel might consider this to be ‘backsliding’ given how well quantum physics works, but it is our contention that an important new development has entered the picture : the discovery that inertia can be interpreted as a reaction force due to scattering of an asymmetric component of the ZPF that appears in accelerated reference frames. In Haisch, Rueda & Puthoff (hereafter, 1994, HRP), we carried out a preliminary analysis that we interpreted as a derivation of Newton’s F=ma from Maxwell’s equations as applied to the ZPF. This has now been generalized as follows : a force, F, applied to a static object must generate an equal and opposite reaction force, back upon the Fr, agent: This is, of course, Newton’s third law and F=-Fr. must be true on the basis of symmetry. If a motive force is applied to a non fixed object, what will happen? We have found that an acceleration-dependent reaction force, Fr, arises from Maxwell’s equations as applied to the ZPF and the assumption that the charged particles in matter (quarks and electrons) scatter this radiation. In the low-velocity limit we find that Fr=-mia, where mi is an invariant scalar with the dimension of mass. It thus appears that F=ma is indeed derivable from Newton’s third law plus Maxwell’s equations. Moreover, in this new derivation we find the correct form for the relativistic 4-force : F=dP/dT (Rueda & Haisch 1997).
Michel would argue that it is this very assumption that there is any charged particle-ZPF interaction that is erroneous.We argue that the issue is not yet settled and that the inertia result provides motivation for further investigation.
2 – QUANTUM ARGUMENTS AND THE CASIMIR FORCE
In Michel’s view a major problem is that there have been ‘five semidistinct concepts’ of the ZPF afoot, and as a result ‘people can argue endlessly past one another.’ This has sometimes been the case, but it is highly debatable ‘that there never has been the open debate and discussion of the sort that accompanied other breakthroughs. . .’ One need only look, for example, at two very comprehensive monographs published recently. From the SED point of view, which presupposes a real ZPF, there is the long and extensive review and contribution to the field by de la Pena & Cetto with extensive analysis and a huge number of (1996) references to published work. This, together with the monograph of on the quantum version of the ZPF Milonni (1994) and its relevance to the foundations of quantum electrodynamics (QED), and references therein, demonstrate a high level of extant discussion and debate. Groups of researchers are seriously involved in ZPF issues and ontology.
Of Michel’s division into five camps, two are concerned with the quantum-theoretical reality of these fields and three with more or less classical analogs. Certainly Michel is correct insofar as the quantum-field-theoretical ‘reality’ of the ZPF is an issue distinct from that of the classical reality of these fields, since the latter has now gained its own raison d’etre through the increasing success of SED. In particular, a recent development in SED has been the derivation of the quantum-mechanical distribution (for a charged particle) entirely from within the classical paradigm by Ibison & Haisch (1996).
Consequently we propose that this revisedclassical ZPF formulation serve as the basis for future comparison between SED and QED, as the foundation of a classical ZPF in its own right and as a useful conceptual tool with which to address issues concerning the impact of the ZPF.
Michel questions whether it is necessary to write the photon Hamiltonian precisely parallel to the harmonic oscillator Hamiltonian such that
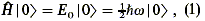
on the basis of which the zero-point state | 0> has energy hw/2 (see Loudon 1983, chap. 4, for detailed discussion of the generation of the quantized Ðeld operators from E and B).
Milonni (1994, chap. 2.6) presents arguments to show why ‘the zero-point Ðeld is not eliminated by dropping its energy from the Hamiltonian’ (Milonni 1994, p.43).
If one does not allow the |0> state to possess a real energy, one runs into problems with the Ñuctuation-dissipation theorem: ‘radiation reaction will cause canonical commutators like [x, px] to decay to zero unless the fluctuatingvacuum field is included, in which case commutators are consistently preserved’ (Milonni 1994, p.81).
Calculating the eigenvalues of the photon momentum operator, one finds (Milonni 1994, p.46)
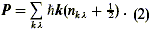
This is important because it allows one to interpret the Casimir force between parallel conducting plates in a very simple way. If in addition to energy there is momentum in the ZPF, then the exclusion of field modes having wavelengths longer than the plate separation creates an imbalance giving rise to an effectivelyzero-point radiation pressure(Milonni 1994, ch. 3.10 ; Milonni Cook, & Goggin, 1988).
Milonni (1994, p.73) concludes: ‘Observable phenomena like the Casimir eect strongly suggest that the vacuum electromagnetic field and its zero-point energy are real physical entities and not mere artifices of the quantum formalism.’ The Casimir force has finally been measured with 5% precision and found to agree with theory (Lamoreaux 1997). There is an intuitively obvious parallel between the Casimir force and the ZPF-based reaction force that we interpret as the inertia of matter.
3. THE COSMOLOGICAL CONSTANT
Michel is correct in pointing out that the ZPF cannot be the manifestation of a cosmological constant, ‘C’, or vice versa. The equivalent mass density of the ZPF is
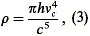
where vc is the presumed effective cutoff of the spectrum. A cosmologically critical density of 10-29 g cm-3 would result from any ZPF extending as a v3 spectrum up to only +- 2 x 1012 Hz, i.e., j +- 160 um in the far-infrared. If the ZPF is to be eective in generating the phenomena discussed herein and by Michel, it must extend orders of magnitude beyond this. We fully agree with that Wesson (1991) the ZPF either does not exist or does not gravitate in the usual way; indeed it cannot gravitate in the usual way. The ZPF is not a candidate source for a cosmological constant. The ZPF, if real, can have nothing to do with ‘C’ and is not, of itself, a source of gravitation.
If inertial mass, originates in ZPF-charge interactions, mi, then, by the principle of equivalence, so must gravitational mass, mg. In this view, gravitation would be a force originating in ZPF-charge interactions analogous to the inertia concept. was the Ðrst to conjecture this Sakharov (1968) interpretation of gravity. If true, gravitation would be unified with the other forces : it would be a manifestation of electromagnetism. If so, there would not be a gravitational field and there would not be a gravitational interaction as such independent of electromagnetism. Gravity would be a derived long-range but fairly minute force in a manner very reminiscent of the van der Waals attractive force among polarizable molecules.
The general relativistic mathematical treatment of gravitation as a spacetime curvature works extremely well.
However, if it could be shown that a dierent theoretical basis can be made analytically equivalent to spacetime curvature, with its prediction of gravitational lensing, black holes, etc., this may reopen the possibility that gravitation should be viewed as an electromagnetically derived force.
The following points are worth noting : (a) general relativity and quantum physics are at present irreconcilable, therefore something substantive is either wrong or missing in our understanding of one or both; (b) the propagation of gravitational waves is not rigorously consistent with spacetime curvature. The issue revolves around whether gravitational waves can be made to vanish in a properly chosen coordinate system. The discovery of apparent gravitational energy loss by the Hulse-Taylor pulsar provides only indirect evidence for the existence of gravitational waves. Theoretical developments and calculations have not yet been performed to examine whether an approach based on the Sakharov ideas would predict gravitational waves, but the (1968) coordinate ambiguities of general relativity should not appear in a ZPF-referenced theory of gravitation.
There were some early pioneering attempts, inspired by Sakharov’s conjecture, to link gravity to the vacuum from a quantum-field-theoretical viewpoint (by Amati, Adler, and others ; see discussion and references in Thorne, & Misner, Wheeler 1973) as well as within SED (seeSurdin 1978).
The first step in developing Sakharov’s conjecture in any detail within the classical context of nonrelativistic SED was the work of Gravity is treated as a residuum Puthoff (1989). force in the manner of the van der Waals forces. Expressed in the most rudimentary way, this can be viewed as follows.
The electric component of the ZPF causes a given charged particle (quark or electron) to oscillate. Such oscillations give rise to secondary electromagnetic fields. An adjacent charged particle will thus experience both the ZPF driving forces causing it to oscillate and, in addition, forces due to the secondary fields produced by the ZPF-driven oscillations of the first particle. Similarly, the ZPF-driven oscillations of the second particle will cause their own secondary fields acting back upon the first particle. The net effect is always an attractive force between the particles. The sign of the charge does not matter; it only affects the phasing of the interactions. Unlike the Coulomb force, which, classically viewed, acts directly between charged particles, this interaction is mediated by extremely minute propagating secondary fields created by the ZPF-driven oscillations, and so is enormously weaker than the Coulomb force. Gravitation, in this view, appears to be a long-range interaction akin to the van der Waals force.
The ZPF-driven ultrarelativistic oscillations were named Zitterbewegung by Schrodinger. The Puthoff analysis consists of two separate parts. In the first, the energy of the Zitterbewegung motion is equated to gravitational mass, mg (after dividing by c2). This leads to a relationship between and electrodynamic parameters that is identical to the mg inertial mass, apart from a factor of 2. This factor HRP mi, of 2 is discussed in the appendix of in which it is HRP, concluded that the Puthoff mg should be reduced by a factor mg of 2, yielding precisely mi = mg.
The second part of Puthoff’s analysis is more controversial. He quantitatively examines the van der Waals force-like interactions between two driven oscillating dipoles and derives an inverse-square force of attraction. This part of the analysis has been challenged by to which Carlip (1993), has responded, but, since problems remain Puthoff (1993) this aspect of the ZPF-gravitation concept (Danley 1994), requires further theoretical development, in particular the implementation of a fully relativistic model.
Clearly the ZPF-inertia and the ZPF-gravitation concepts must stand or fall together, given the principle of equivalence. However, that being the case, the Sakharov-Puthoff -type gravity concept does legitimately refute the objection that ‘the ZPF cannot be a real electromagnetic field since the energy density of this field would be enormous and thereby act as a cosmological constant, ‘C’, of enormous proportions that would curve the Universe into something microscopic in size.’ This cannot happen in the Sakharov-Puthoff view. This situation is clearly ruled out by the elementary fact that, in this view, the ZPF cannot act upon itself to gravitate. Gravitation is not caused by the mere presence of the ZPF, but rather by secondary motions of charged particles driven by the ZPF. In this view it is impossible for the ZPF to give rise to a cosmological constant. (The possibility of nongravitating vacuum energy has recently been investigated in quantum cosmology in the framework of the modiÐed Born-Oppenheimer approximation by Datta 1995.)
The other side of this argument is of course that, as electromagnetic radiation is not made of polarizable entities, one might naively no longer expect deviation of light rays by massive bodies. We speculate, however, that such deviation will be part of a fully relativistic theory that properly takes into account, besides the ZPF, the polarization of the Dirac vacuum when light rays pass through the particle-antiparticle Dirac sea. It should act, in effect, as a medium with an index of refraction modified in the vicinity of massive objects. This is very much in line with the original concept. Indeed, within a more general Sakharov (1968) field-theoretical framework one would expect that the role of the ZPF in the inertia and gravitation developments mentioned above will be played by a more general quantum vacuum field.
B. H. wishes to thank Professor J. Trumper and the Max-Planck-Institut fur extraterrestrische Physik for hospitality during several stays as a visiting fellow. A. R. acknowledges many stimulating exchanges with D. C. Cole. B. H. and A. R. also acknowledge NASA contract NASW-5050 for support of this research.
References:
– Carlip, S. 1993, Phys. Rev., 47, 3452
– Danley, K. 1994, Ph.D. thesis, California State Univ. Long Beach
– Datta, D. P. 1995, Classical Quantum Gravity, 12, 2499
– Davies, P. C. W. & Betts, D. S. 1994, Quantum Mechanics (2d ed. ; Boston Routledge)
– de la Pena, L., & Cetto, A. M. 1996, The Quantum Dice: An Introductionto Stochastic Electrodynamics (Dordrecht: Kluwer)
– Haisch, B., Rueda, A., & Putho, H. E. 1994, Phys. Rev. A, 49, 678 (HRP)
– Ibison, M., & Haisch, B. 1996, Phys. Rev. A, 54,2737
– Lamoreaux, S. K. 1997, Phys. Rev. Lett., 78,5
– Loudon, R. 1983, The Quantum Theory of Light (Oxford:Claredon)
– Michel, F. C. 1996, ApJ, 466, 660
– Milonni, P. W. 1994, The Quantum Vacuum: An Introduction toQuantum Electrodynamics (New York: Academic)
– Milonni, P. W., Cook, R. J., & Goggin, M. E. 1988, Phys. Rev. A, 38, 1621
– Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: Freeman)
– Puthoff, H. E. 1989, Phys. Rev. A, 39, 2333
-Puthoff, H. E. 1993, Phys. Rev. A, 47, 3454
-Rueda, A., & Haisch, B. M. 1997, Phys. Rev. A, submitted
– Sakharov, A. D. 1968, Dokl. Akad, Nauk SSSR (Soviet Phys. Dokl.), 12, 1040
– Surdin, M. 1978, Found. Phys., 8, 341
– Wesson, P. S. 1991, ApJ, 387, 466